Skip to contents

Posterior Distribution of the Indirect Effect Centrality Over a Specific Time Interval or a Range of Time Intervals

Source: R/cTMed-posterior-indirect-central.R
PosteriorIndirectCentral.Rd

This function generates a posterior distribution of the indirect effect centrality over a specific time interval \(\Delta t\) or a range of time intervals using the posterior distribution of the first-order stochastic differential equation model drift matrix \(\boldsymbol{\Phi}\).

Usage

PosteriorIndirectCentral(phi, delta_t, ncores = NULL, tol = 0.01)

Arguments

phi

List of numeric matrices. Each element of the list is a sample from the posterior distribution of the drift matrix (\(\boldsymbol{\Phi}\)). Each matrix should have row and column names pertaining to the variables in the system.

delta_t

Numeric. Time interval (\(\Delta t\)).

ncores

Positive integer. Number of cores to use. If ncores = NULL, use a single core. Consider using multiple cores when number of replications R is a large value.

tol

Numeric. Smallest possible time interval to allow.

Value

Returns an object of class ctmedmc which is a list with the following elements:

call

Function call.

args

Function arguments.

fun

Function used ("PosteriorIndirectCentral").

output

A list the length of which is equal to the length of delta_t.

Each element in the output list has the following elements:

est

Mean of the posterior distribution of the total, direct, and indirect effects.

thetahatstar

Posterior distribution of the total, direct, and indirect effects.

Details

See TotalCentral() for more details.

References

Bollen, K. A. (1987). Total, direct, and indirect effects in structural equation models. Sociological Methodology, 17, 37. doi:10.2307/271028

Deboeck, P. R., & Preacher, K. J. (2015). No need to be discrete: A method for continuous time mediation analysis. Structural Equation Modeling: A Multidisciplinary Journal, 23 (1), 61–75. doi:10.1080/10705511.2014.973960

Pesigan, I. J. A., Russell, M. A., & Chow, S.-M. (2025). Inferences and effect sizes for direct, indirect, and total effects in continuous-time mediation models. Psychological Methods. doi:10.1037/met0000779

Ryan, O., & Hamaker, E. L. (2021). Time to intervene: A continuous-time approach to network analysis and centrality. Psychometrika, 87 (1), 214–252. doi:10.1007/s11336-021-09767-0

See also

Other Continuous-Time Mediation Functions: BootBeta(), BootBetaStd(), BootIndirectCentral(), BootMed(), BootMedStd(), BootTotalCentral(), DeltaBeta(), DeltaBetaStd(), DeltaIndirectCentral(), DeltaMed(), DeltaMedStd(), DeltaTotalCentral(), Direct(), DirectStd(), Indirect(), IndirectCentral(), IndirectStd(), MCBeta(), MCBetaStd(), MCIndirectCentral(), MCMed(), MCMedStd(), MCPhi(), MCPhiSigma(), MCTotalCentral(), Med(), MedStd(), PosteriorBeta(), PosteriorMed(), PosteriorTotalCentral(), Total(), TotalCentral(), TotalStd(), Trajectory()

Author

Ivan Jacob Agaloos Pesigan

Examples

phi <- matrix(
  data = c(
    -0.357, 0.771, -0.450,
    0.0, -0.511, 0.729,
    0, 0, -0.693
  ),
  nrow = 3
)
colnames(phi) <- rownames(phi) <- c("x", "m", "y")
vcov_phi_vec <- matrix(
  data = c(
    0.00843, 0.00040, -0.00151,
    -0.00600, -0.00033, 0.00110,
    0.00324, 0.00020, -0.00061,
    0.00040, 0.00374, 0.00016,
    -0.00022, -0.00273, -0.00016,
    0.00009, 0.00150, 0.00012,
    -0.00151, 0.00016, 0.00389,
    0.00103, -0.00007, -0.00283,
    -0.00050, 0.00000, 0.00156,
    -0.00600, -0.00022, 0.00103,
    0.00644, 0.00031, -0.00119,
    -0.00374, -0.00021, 0.00070,
    -0.00033, -0.00273, -0.00007,
    0.00031, 0.00287, 0.00013,
    -0.00014, -0.00170, -0.00012,
    0.00110, -0.00016, -0.00283,
    -0.00119, 0.00013, 0.00297,
    0.00063, -0.00004, -0.00177,
    0.00324, 0.00009, -0.00050,
    -0.00374, -0.00014, 0.00063,
    0.00495, 0.00024, -0.00093,
    0.00020, 0.00150, 0.00000,
    -0.00021, -0.00170, -0.00004,
    0.00024, 0.00214, 0.00012,
    -0.00061, 0.00012, 0.00156,
    0.00070, -0.00012, -0.00177,
    -0.00093, 0.00012, 0.00223
  ),
  nrow = 9
)

phi <- MCPhi(
  phi = phi,
  vcov_phi_vec = vcov_phi_vec,
  R = 1000L
)$output

# Specific time interval ----------------------------------------------------
PosteriorIndirectCentral(
  phi = phi,
  delta_t = 1
)
#> Call:
#> PosteriorIndirectCentral(phi = phi, delta_t = 1)
#> 
#> Indirect Effect Centrality
#> 
#>   variable interval    est     se    R    2.5%  97.5%
#> 1        x        1 0.0005 0.0189 1000 -0.0325 0.0386
#> 2        m        1 0.1667 0.0176 1000  0.1328 0.2023
#> 3        y        1 0.0007 0.0135 1000 -0.0233 0.0277

# Range of time intervals ---------------------------------------------------
posterior <- PosteriorIndirectCentral(
  phi = phi,
  delta_t = 1:5
)

# Methods -------------------------------------------------------------------
# PosteriorIndirectCentral has a number of methods including
# print, summary, confint, and plot
print(posterior)
#> Call:
#> PosteriorIndirectCentral(phi = phi, delta_t = 1:5)
#> 
#> Indirect Effect Centrality
#> 
#>    variable interval     est     se    R    2.5%  97.5%
#> 1         x        1  0.0005 0.0189 1000 -0.0325 0.0386
#> 2         m        1  0.1667 0.0176 1000  0.1328 0.2023
#> 3         y        1  0.0007 0.0135 1000 -0.0233 0.0277
#> 4         x        2  0.0009 0.0370 1000 -0.0670 0.0749
#> 5         m        2  0.3999 0.0465 1000  0.3125 0.4956
#> 6         y        2  0.0015 0.0311 1000 -0.0527 0.0640
#> 7         x        3  0.0005 0.0454 1000 -0.0869 0.0874
#> 8         m        3  0.5431 0.0719 1000  0.4176 0.6970
#> 9         y        3  0.0014 0.0467 1000 -0.0851 0.0936
#> 10        x        4 -0.0001 0.0506 1000 -0.1030 0.0960
#> 11        m        4  0.5864 0.0881 1000  0.4427 0.7814
#> 12        y        4  0.0006 0.0620 1000 -0.1189 0.1163
#> 13        x        5 -0.0003 0.0549 1000 -0.1129 0.1041
#> 14        m        5  0.5598 0.0947 1000  0.4126 0.7809
#> 15        y        5 -0.0004 0.0763 1000 -0.1484 0.1444
summary(posterior)
#> Call:
#> PosteriorIndirectCentral(phi = phi, delta_t = 1:5)
#> 
#> Indirect Effect Centrality
#> 
#>    variable interval     est     se    R    2.5%  97.5%
#> 1         x        1  0.0005 0.0189 1000 -0.0325 0.0386
#> 2         m        1  0.1667 0.0176 1000  0.1328 0.2023
#> 3         y        1  0.0007 0.0135 1000 -0.0233 0.0277
#> 4         x        2  0.0009 0.0370 1000 -0.0670 0.0749
#> 5         m        2  0.3999 0.0465 1000  0.3125 0.4956
#> 6         y        2  0.0015 0.0311 1000 -0.0527 0.0640
#> 7         x        3  0.0005 0.0454 1000 -0.0869 0.0874
#> 8         m        3  0.5431 0.0719 1000  0.4176 0.6970
#> 9         y        3  0.0014 0.0467 1000 -0.0851 0.0936
#> 10        x        4 -0.0001 0.0506 1000 -0.1030 0.0960
#> 11        m        4  0.5864 0.0881 1000  0.4427 0.7814
#> 12        y        4  0.0006 0.0620 1000 -0.1189 0.1163
#> 13        x        5 -0.0003 0.0549 1000 -0.1129 0.1041
#> 14        m        5  0.5598 0.0947 1000  0.4126 0.7809
#> 15        y        5 -0.0004 0.0763 1000 -0.1484 0.1444
confint(posterior, level = 0.95)
#>    variable interval       2.5 %     97.5 %
#> 1         x        1 -0.03250983 0.03857900
#> 2         m        1  0.13278798 0.20227734
#> 3         y        1 -0.02331382 0.02772267
#> 4         x        2 -0.06695886 0.07488156
#> 5         m        2  0.31252172 0.49556382
#> 6         y        2 -0.05271001 0.06397910
#> 7         x        3 -0.08690579 0.08744346
#> 8         m        3  0.41756817 0.69698988
#> 9         y        3 -0.08512262 0.09356038
#> 10        x        4 -0.10301180 0.09604241
#> 11        m        4  0.44270165 0.78135684
#> 12        y        4 -0.11892150 0.11625868
#> 13        x        5 -0.11286648 0.10411650
#> 14        m        5  0.41257630 0.78088527
#> 15        y        5 -0.14842636 0.14441182
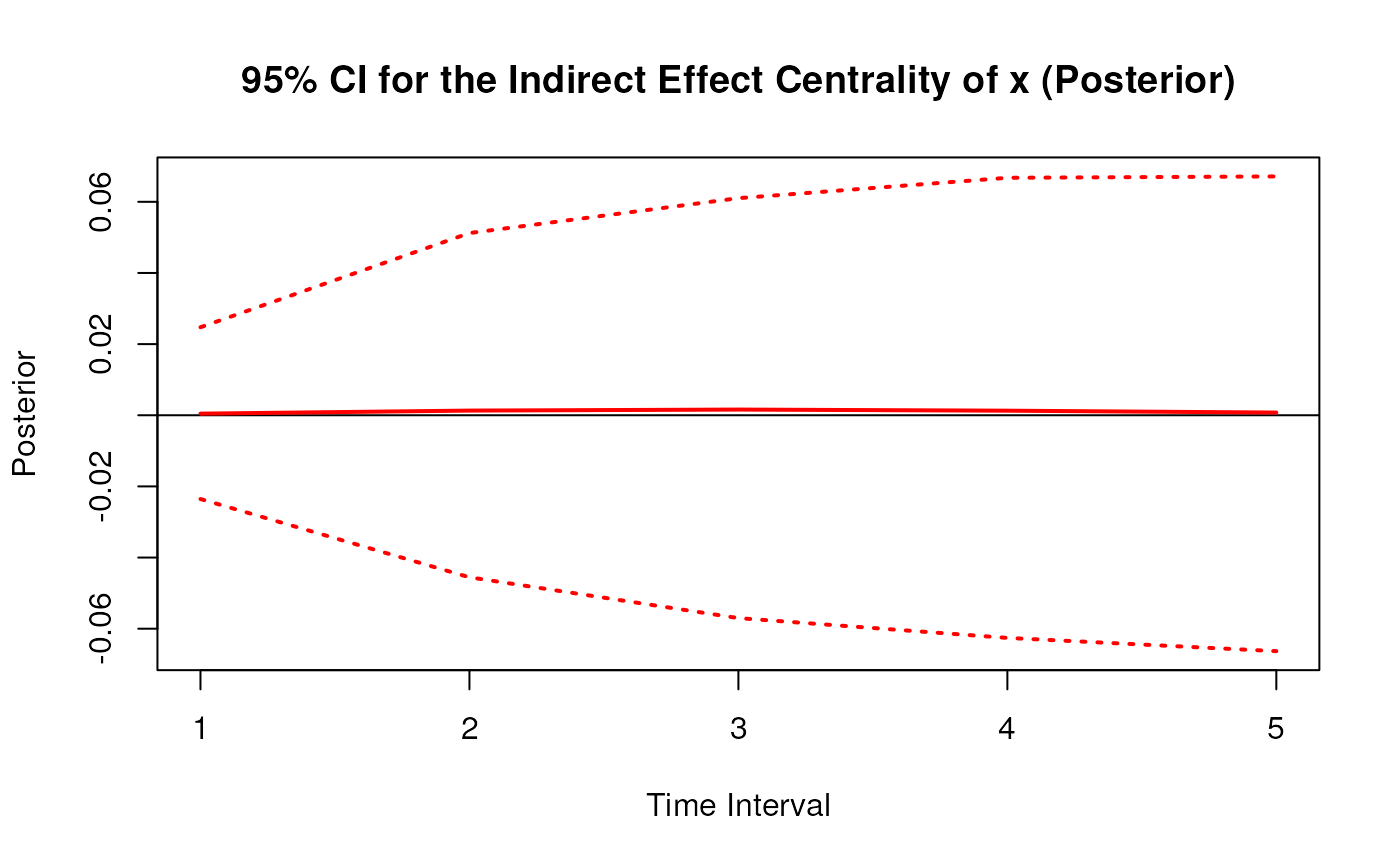
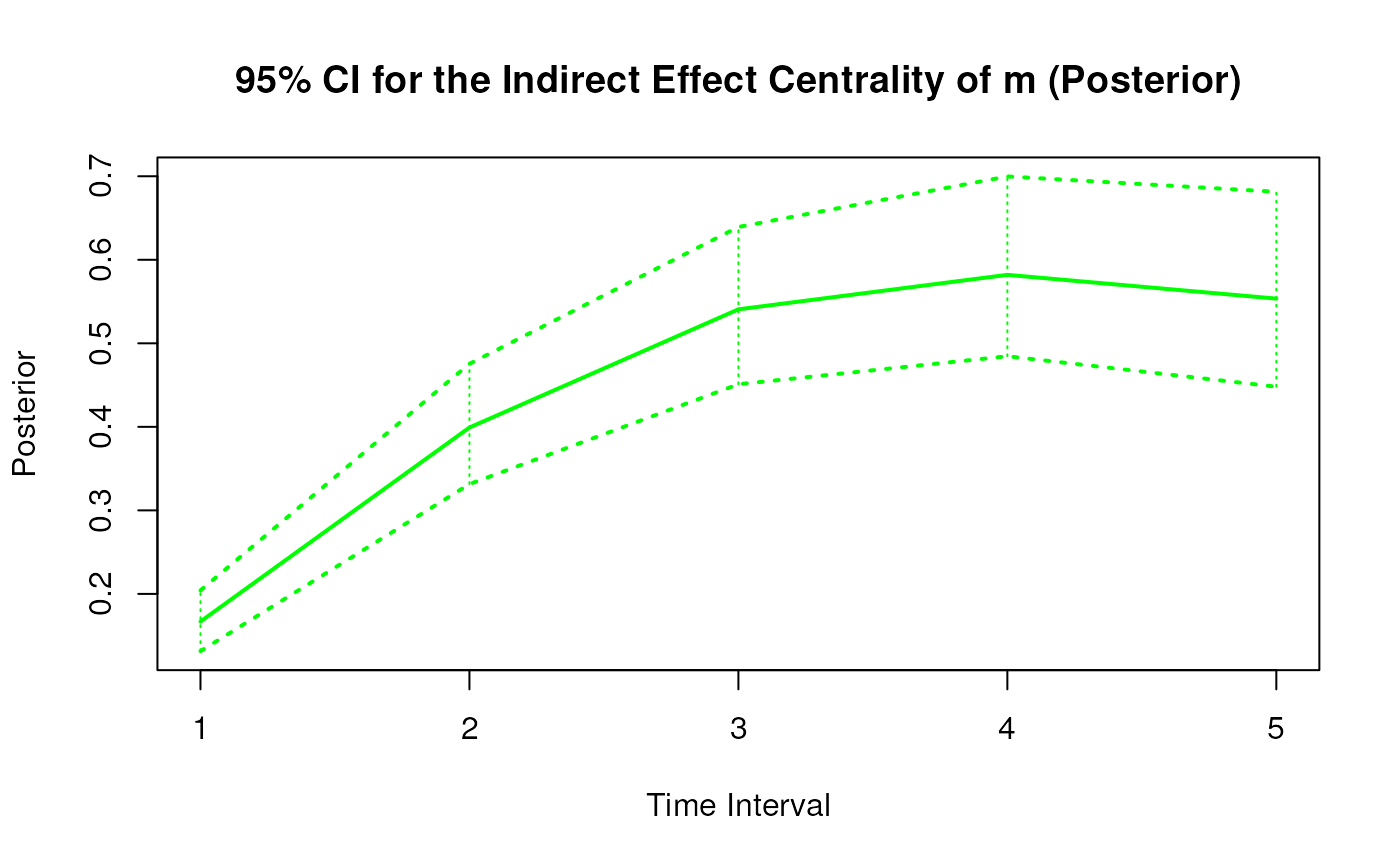
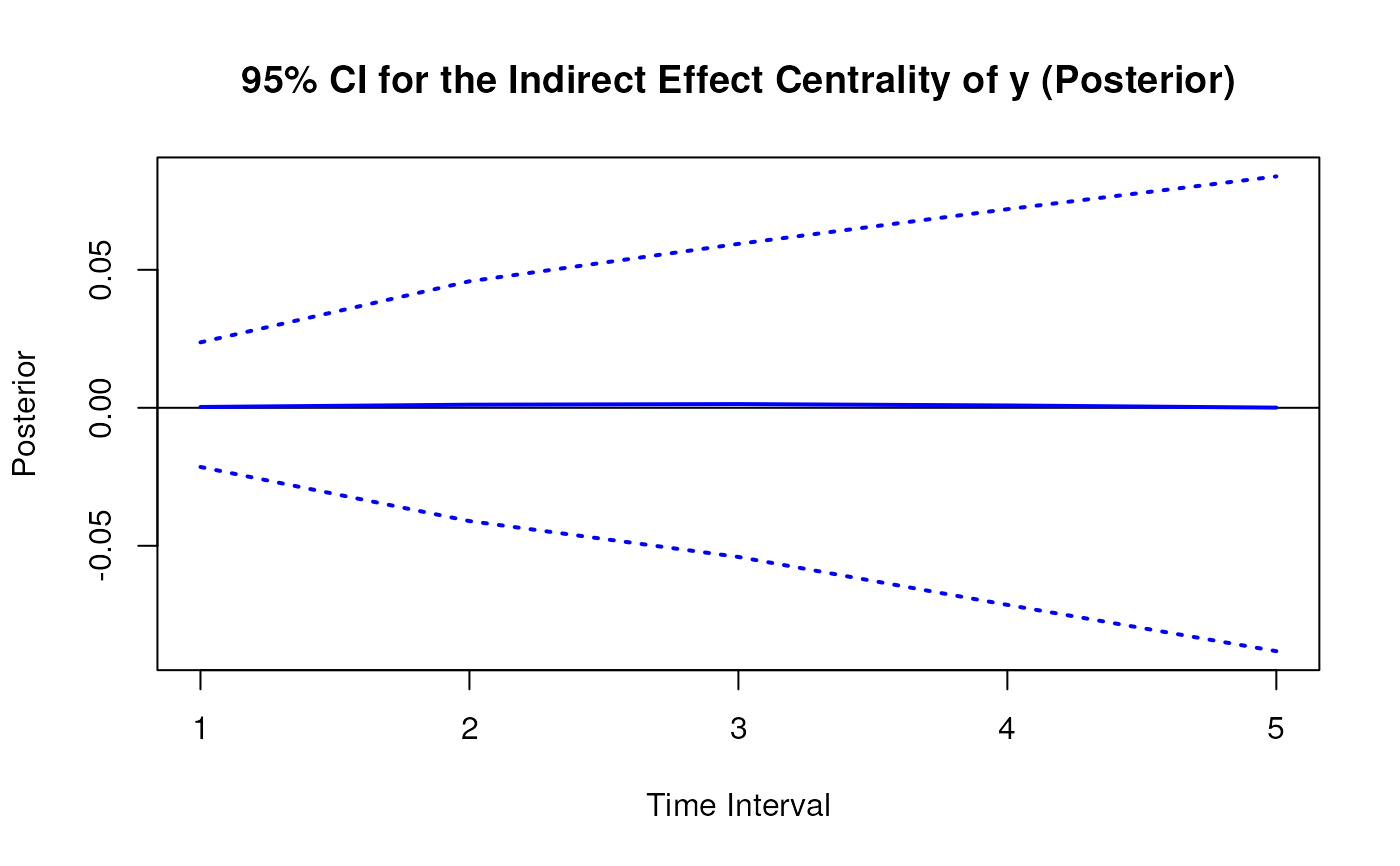
plot(posterior)