Indirect Effect Centrality

Indirect Effect Centrality

Usage

IndirectCentral(phi, delta_t)

Arguments

phi

Numeric matrix. The drift matrix (\(\boldsymbol{\Phi}\)). phi should have row and column names pertaining to the variables in the system.

delta_t

Vector of positive numbers. Time interval (\(\Delta t\)).

Value

Returns an object of class ctmedmed which is a list with the following elements:

call

Function call.

args

Function arguments.

fun

Function used ("IndirectCentral").

output

A matrix of indirect effect centrality.

Details

Indirect effect centrality is the sum of all possible indirect effects between different pairs of variables in which a specific variable serves as the only mediator.

References

Bollen, K. A. (1987). Total, direct, and indirect effects in structural equation models. Sociological Methodology, 17, 37. doi:10.2307/271028

Deboeck, P. R., & Preacher, K. J. (2015). No need to be discrete: A method for continuous time mediation analysis. Structural Equation Modeling: A Multidisciplinary Journal, 23 (1), 61–75. doi:10.1080/10705511.2014.973960

Ryan, O., & Hamaker, E. L. (2021). Time to intervene: A continuous-time approach to network analysis and centrality. Psychometrika, 87 (1), 214–252. doi:10.1007/s11336-021-09767-0

See also

Other Continuous Time Mediation Functions: DeltaBeta(), DeltaIndirectCentral(), DeltaMed(), DeltaTotalCentral(), Direct(), Indirect(), MCBeta(), MCIndirectCentral(), MCMed(), MCPhi(), MCTotalCentral(), Med(), PosteriorBeta(), PosteriorIndirectCentral(), PosteriorMed(), PosteriorPhi(), PosteriorTotalCentral(), Total(), TotalCentral(), Trajectory()

Author

Ivan Jacob Agaloos Pesigan

Examples

phi <- matrix(
  data = c(
    -0.357, 0.771, -0.450,
    0.0, -0.511, 0.729,
    0, 0, -0.693
  ),
  nrow = 3
)
colnames(phi) <- rownames(phi) <- c("x", "m", "y")

# Specific time interval ----------------------------------------------------
IndirectCentral(
  phi = phi,
  delta_t = 1
)
#> 
#> Indirect Effect Centrality
#> 
#>      interval x      m y
#> [1,]        1 0 0.1674 0

# Range of time intervals ---------------------------------------------------
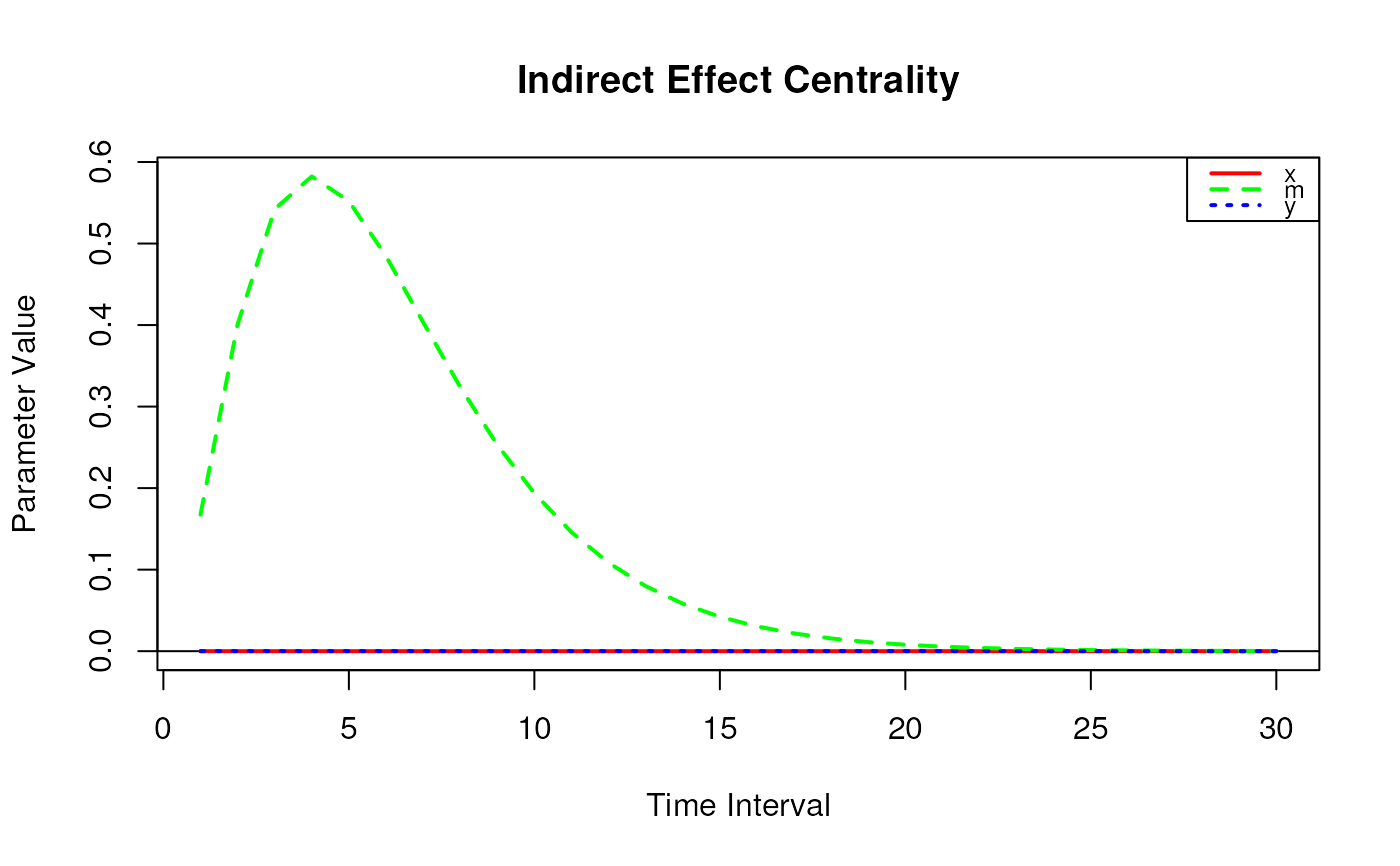
indirect_central <- IndirectCentral(
  phi = phi,
  delta_t = 1:30
)
plot(indirect_central)


# Methods -------------------------------------------------------------------
# IndirectCentral has a number of methods including
# print, summary, and plot
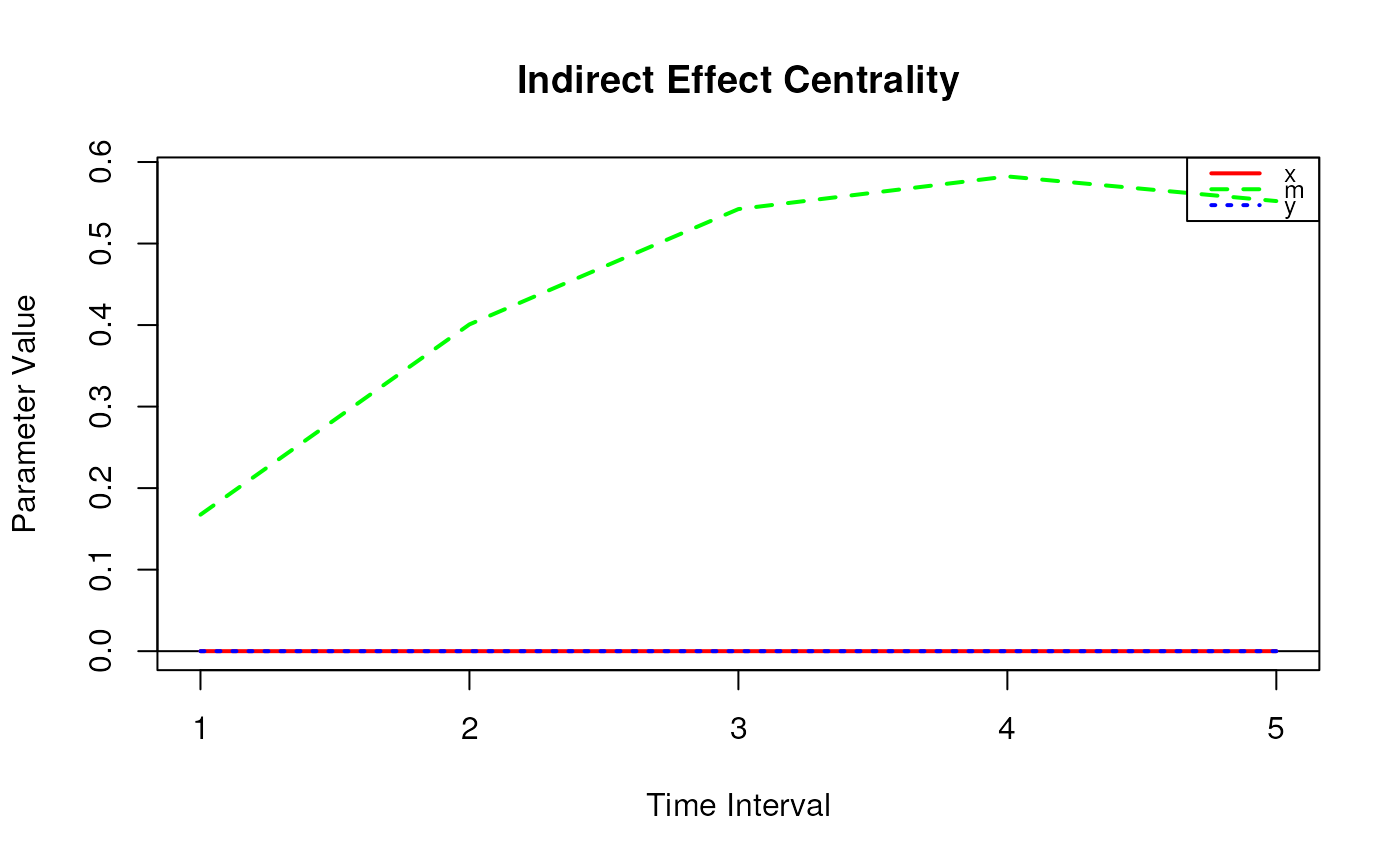
indirect_central <- IndirectCentral(
  phi = phi,
  delta_t = 1:5
)
print(indirect_central)
#> 
#> Indirect Effect Centrality
#> 
#>      interval x      m y
#> [1,]        1 0 0.1674 0
#> [2,]        2 0 0.4008 0
#> [3,]        3 0 0.5423 0
#> [4,]        4 0 0.5823 0
#> [5,]        5 0 0.5521 0
summary(indirect_central)
#>      interval x      m y
#> [1,]        1 0 0.1674 0
#> [2,]        2 0 0.4008 0
#> [3,]        3 0 0.5423 0
#> [4,]        4 0 0.5823 0
#> [5,]        5 0 0.5521 0
plot(indirect_central)