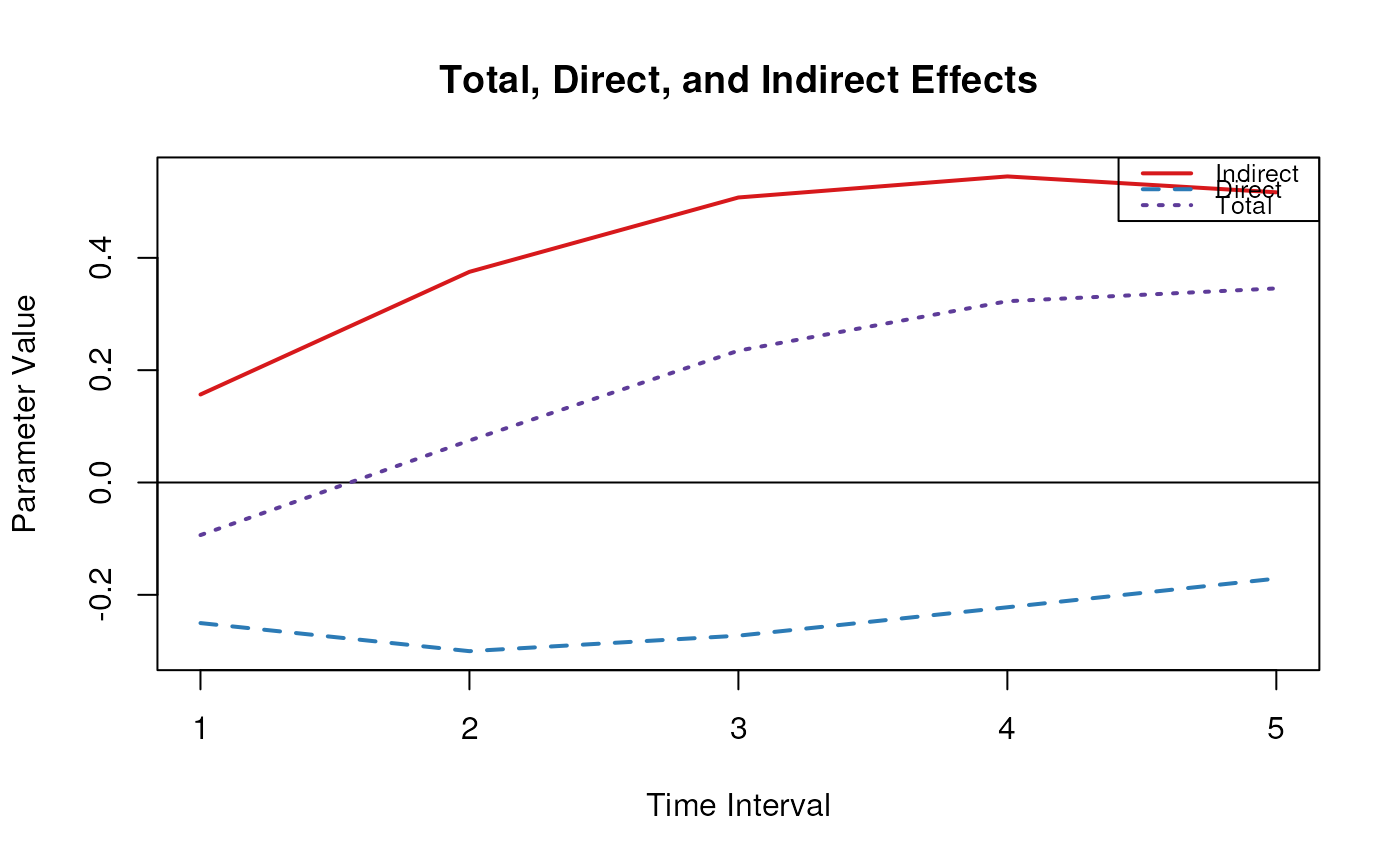
Standardized Total, Direct, and Indirect Effects of X on Y Through M Over a Specific Time Interval or a Range of Time Intervals

This function computes the standardized total, direct, and indirect effects of the independent variable \(X\) on the dependent variable \(Y\) through mediator variables \(\mathbf{m}\) over a specific time interval \(\Delta t\) or a range of time intervals using the first-order stochastic differential equation model's drift matrix \(\boldsymbol{\Phi}\) and process noise covariance matrix \(\boldsymbol{\Sigma}\).

Usage

MedStd(phi, sigma, delta_t, from, to, med, tol = 0.01)

Arguments

phi

Numeric matrix. The drift matrix (\(\boldsymbol{\Phi}\)). phi should have row and column names pertaining to the variables in the system.

sigma

Numeric matrix. The process noise covariance matrix (\(\boldsymbol{\Sigma}\)).

delta_t

Numeric. Time interval (\(\Delta t\)).

from

Character string. Name of the independent variable \(X\) in phi.

to

Character string. Name of the dependent variable \(Y\) in phi.

med

Character vector. Name/s of the mediator variable/s in phi.

tol

Numeric. Smallest possible time interval to allow.

Value

Returns an object of class ctmedmed which is a list with the following elements:

call

Function call.

args

Function arguments.

fun

Function used ("MedStd").

output

A standardized matrix of total, direct, and indirect effects.

Details

See TotalStd(), DirectStd(), and IndirectStd() for more details.

References

Bollen, K. A. (1987). Total, direct, and indirect effects in structural equation models. Sociological Methodology, 17, 37. doi:10.2307/271028

Deboeck, P. R., & Preacher, K. J. (2015). No need to be discrete: A method for continuous time mediation analysis. Structural Equation Modeling: A Multidisciplinary Journal, 23 (1), 61–75. doi:10.1080/10705511.2014.973960

Pesigan, I. J. A., Russell, M. A., & Chow, S.-M. (2025). Inferences and effect sizes for direct, indirect, and total effects in continuous-time mediation models. Psychological Methods. doi:10.1037/met0000779

Ryan, O., & Hamaker, E. L. (2021). Time to intervene: A continuous-time approach to network analysis and centrality. Psychometrika, 87 (1), 214–252. doi:10.1007/s11336-021-09767-0

See also

Other Continuous-Time Mediation Functions: BootBeta(), BootBetaStd(), BootIndirectCentral(), BootMed(), BootMedStd(), BootTotalCentral(), DeltaBeta(), DeltaBetaStd(), DeltaIndirectCentral(), DeltaMed(), DeltaMedStd(), DeltaTotalCentral(), Direct(), DirectStd(), Indirect(), IndirectCentral(), IndirectStd(), MCBeta(), MCBetaStd(), MCIndirectCentral(), MCMed(), MCMedStd(), MCPhi(), MCPhiSigma(), MCTotalCentral(), Med(), PosteriorBeta(), PosteriorIndirectCentral(), PosteriorMed(), PosteriorTotalCentral(), Total(), TotalCentral(), TotalStd(), Trajectory()

Author

Ivan Jacob Agaloos Pesigan

Examples

phi <- matrix(
  data = c(
    -0.357, 0.771, -0.450,
    0.0, -0.511, 0.729,
    0, 0, -0.693
  ),
  nrow = 3
)
colnames(phi) <- rownames(phi) <- c("x", "m", "y")
sigma <- matrix(
  data = c(
    0.24455556, 0.02201587, -0.05004762,
    0.02201587, 0.07067800, 0.01539456,
    -0.05004762, 0.01539456, 0.07553061
  ),
  nrow = 3
)

# Specific time interval ----------------------------------------------------
MedStd(
  phi = phi,
  sigma = sigma,
  delta_t = 1,
  from = "x",
  to = "y",
  med = "m"
)
#> Call:
#> MedStd(phi = phi, sigma = sigma, delta_t = 1, from = "x", to = "y", 
#>     med = "m")
#> 
#> Total, Direct, and Indirect Effects
#> 
#>      interval   total  direct indirect
#> [1,]        1 -0.1069 -0.2858   0.1789

# Range of time intervals ---------------------------------------------------
med <- MedStd(
  phi = phi,
  sigma = sigma,
  delta_t = 1:30,
  from = "x",
  to = "y",
  med = "m"
)
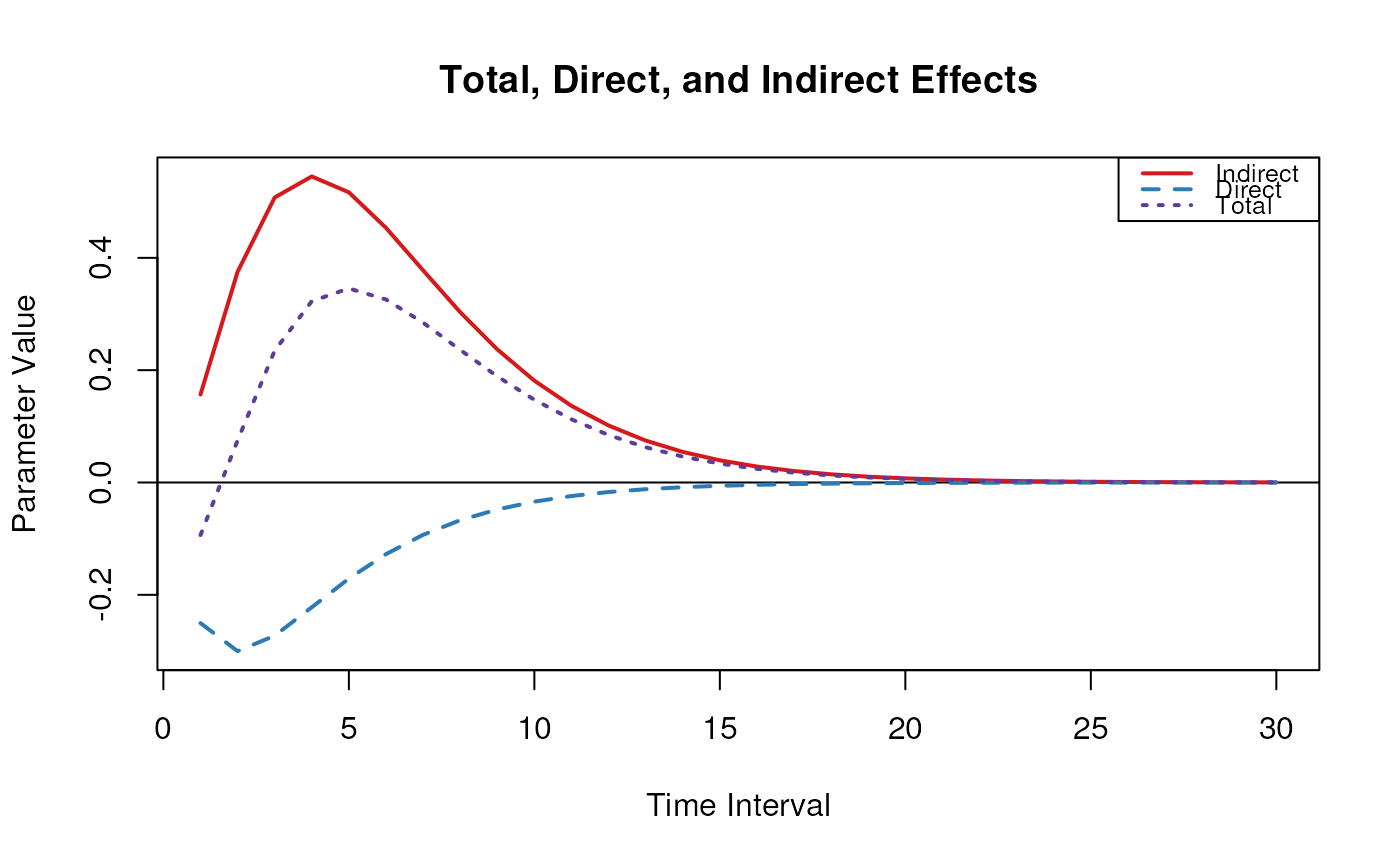
plot(med)


# Methods -------------------------------------------------------------------
# MedStd has a number of methods including
# print, summary, and plot
med <- MedStd(
  phi = phi,
  sigma = sigma,
  delta_t = 1:5,
  from = "x",
  to = "y",
  med = "m"
)
print(med)
#> Call:
#> MedStd(phi = phi, sigma = sigma, delta_t = 1:5, from = "x", to = "y", 
#>     med = "m")
#> 
#> Total, Direct, and Indirect Effects
#> 
#>      interval   total  direct indirect
#> [1,]        1 -0.1069 -0.2858   0.1789
#> [2,]        2  0.0854 -0.3429   0.4283
#> [3,]        3  0.2680 -0.3114   0.5794
#> [4,]        4  0.3686 -0.2537   0.6222
#> [5,]        5  0.3946 -0.1954   0.5899
summary(med)
#> Call:
#> MedStd(phi = phi, sigma = sigma, delta_t = 1:5, from = "x", to = "y", 
#>     med = "m")
#> 
#> Total, Direct, and Indirect Effects
#> 
#>      interval   total  direct indirect
#> [1,]        1 -0.1069 -0.2858   0.1789
#> [2,]        2  0.0854 -0.3429   0.4283
#> [3,]        3  0.2680 -0.3114   0.5794
#> [4,]        4  0.3686 -0.2537   0.6222
#> [5,]        5  0.3946 -0.1954   0.5899
plot(med)