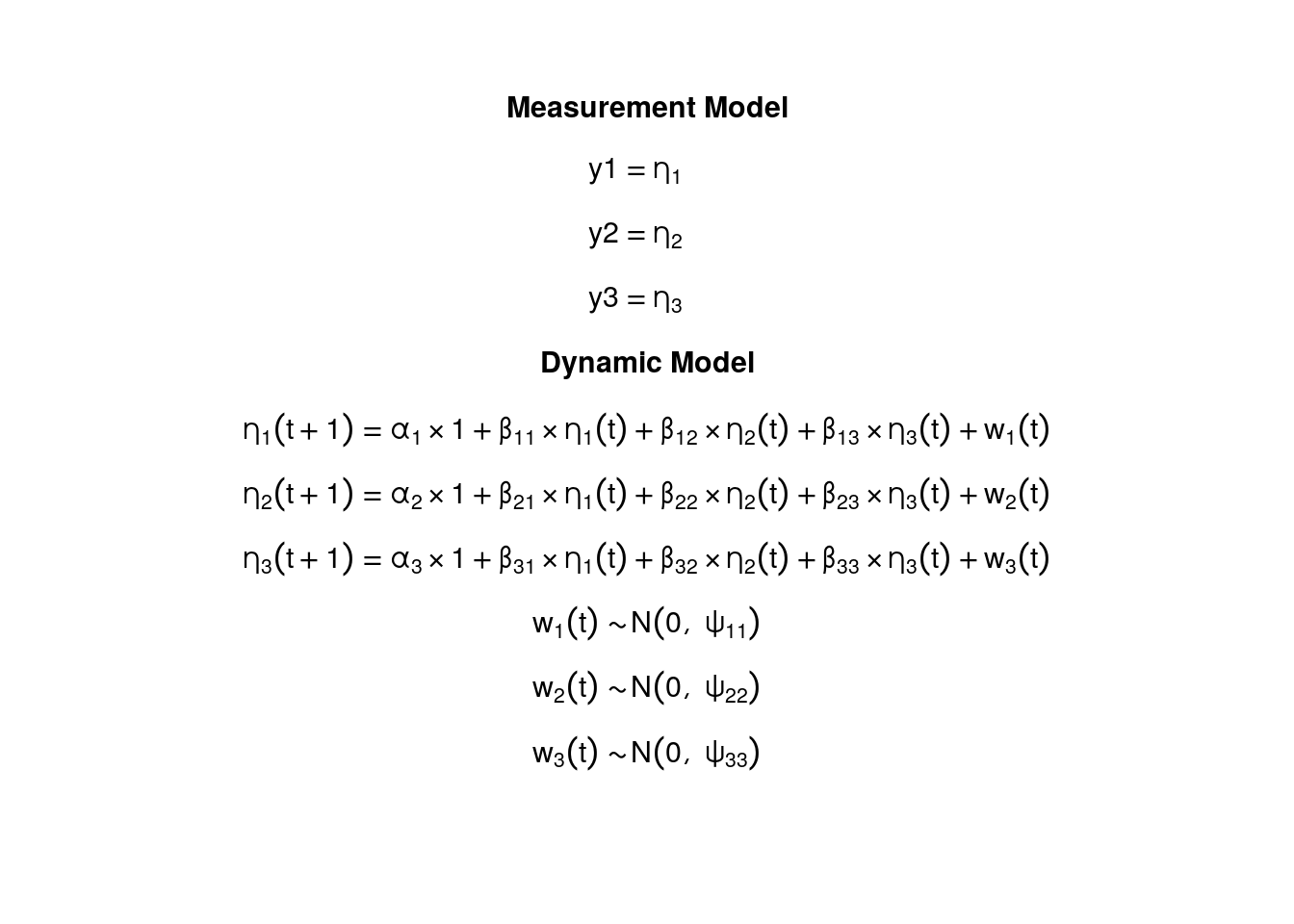Model
The measurement model is given by \[\begin{equation}
\mathbf{y}_{i, t}
=
\boldsymbol{\eta}_{i, t}
\end{equation}\] where \(\mathbf{y}_{i, t}\) represents a vector of observed variables and \(\boldsymbol{\eta}_{i, t}\) a vector of latent variables for individual \(i\) and time \(t\) . Since the observed and latent variables are equal, we only generate data from the dynamic structure.
The dynamic structure is given by \[\begin{equation}
\boldsymbol{\eta}_{i, t}
=
\boldsymbol{\alpha}
+
\boldsymbol{\beta}
\boldsymbol{\eta}_{i, t - 1}
+
\boldsymbol{\zeta}_{i, t},
\quad
\mathrm{with}
\quad
\boldsymbol{\zeta}_{i, t}
\sim
\mathcal{N}
\left(
\mathbf{0},
\boldsymbol{\Psi}
\right)
\end{equation}\] where \(\boldsymbol{\eta}_{i, t}\) , \(\boldsymbol{\eta}_{i, t - 1}\) , and \(\boldsymbol{\zeta}_{i, t}\) are random variables, and \(\boldsymbol{\alpha}\) , \(\boldsymbol{\beta}\) , and \(\boldsymbol{\Psi}\) are model parameters. Here, \(\boldsymbol{\eta}_{i, t}\) is a vector of latent variables at time \(t\) and individual \(i\) , \(\boldsymbol{\eta}_{i, t - 1}\) represents a vector of latent variables at time \(t - 1\) and individual \(i\) , and \(\boldsymbol{\zeta}_{i, t}\) represents a vector of dynamic noise at time \(t\) and individual \(i\) . \(\boldsymbol{\alpha}\) denotes a vector of intercepts, \(\boldsymbol{\beta}\) a matrix of autoregression and cross regression coefficients, and \(\boldsymbol{\Psi}\) the covariance matrix of \(\boldsymbol{\zeta}_{i, t}\) .
An alternative representation of the dynamic noise is given by \[\begin{equation}
\boldsymbol{\zeta}_{i, t}
=
\boldsymbol{\Psi}^{\frac{1}{2}}
\mathbf{z}_{i, t},
\quad
\mathrm{with}
\quad
\mathbf{z}_{i, t}
\sim
\mathcal{N}
\left(
\mathbf{0},
\mathbf{I}
\right)
\end{equation}\] where \(\left( \boldsymbol{\Psi}^{\frac{1}{2}} \right) \left( \boldsymbol{\Psi}^{\frac{1}{2}} \right)^{\prime} = \boldsymbol{\Psi}\) .
Data Generation
Notation
Let \(t = 1000\) be the number of time points and \(n = 5\) be the number of individuals.
Let the initial condition \(\boldsymbol{\eta}_{0}\) be given by
\[\begin{equation}
\boldsymbol{\eta}_{0} \sim \mathcal{N} \left( \boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}, \boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0} \right)
\end{equation}\]
\[\begin{equation}
\boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}
=
\left(
\begin{array}{c}
0 \\
0 \\
0 \\
\end{array}
\right)
\end{equation}\]
\[\begin{equation}
\boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0}
=
\left(
\begin{array}{ccc}
1 & 0.2 & 0.2 \\
0.2 & 1 & 0.2 \\
0.2 & 0.2 & 1 \\
\end{array}
\right) .
\end{equation}\]
Let the constant vector \(\boldsymbol{\alpha}\) be given by
\[\begin{equation}
\boldsymbol{\alpha}
=
\left(
\begin{array}{c}
0 \\
0 \\
0 \\
\end{array}
\right) .
\end{equation}\]
Let the transition matrix \(\boldsymbol{\beta}\) be given by
\[\begin{equation}
\boldsymbol{\beta}
=
\left(
\begin{array}{ccc}
0.7 & 0 & 0 \\
0.5 & 0.6 & 0 \\
-0.1 & 0.4 & 0.5 \\
\end{array}
\right) .
\end{equation}\]
Let the dynamic process noise \(\boldsymbol{\Psi}\) be given by
\[\begin{equation}
\boldsymbol{\Psi}
=
\left(
\begin{array}{ccc}
0.1 & 0 & 0 \\
0 & 0.1 & 0 \\
0 & 0 & 0.1 \\
\end{array}
\right) .
\end{equation}\]
R Function Arguments
[,1] [,2] [,3]
[1,] 1.0 0.2 0.2
[2,] 0.2 1.0 0.2
[3,] 0.2 0.2 1.0
sigma0_l # sigma0_l <- t(chol(sigma0))
[,1] [,2] [,3]
[1,] 1.0 0.0000000 0.0000000
[2,] 0.2 0.9797959 0.0000000
[3,] 0.2 0.1632993 0.9660918
[,1] [,2] [,3]
[1,] 0.7 0.0 0.0
[2,] 0.5 0.6 0.0
[3,] -0.1 0.4 0.5
[,1] [,2] [,3]
[1,] 0.1 0.0 0.0
[2,] 0.0 0.1 0.0
[3,] 0.0 0.0 0.1
psi_l # psi_l <- t(chol(psi))
[,1] [,2] [,3]
[1,] 0.3162278 0.0000000 0.0000000
[2,] 0.0000000 0.3162278 0.0000000
[3,] 0.0000000 0.0000000 0.3162278
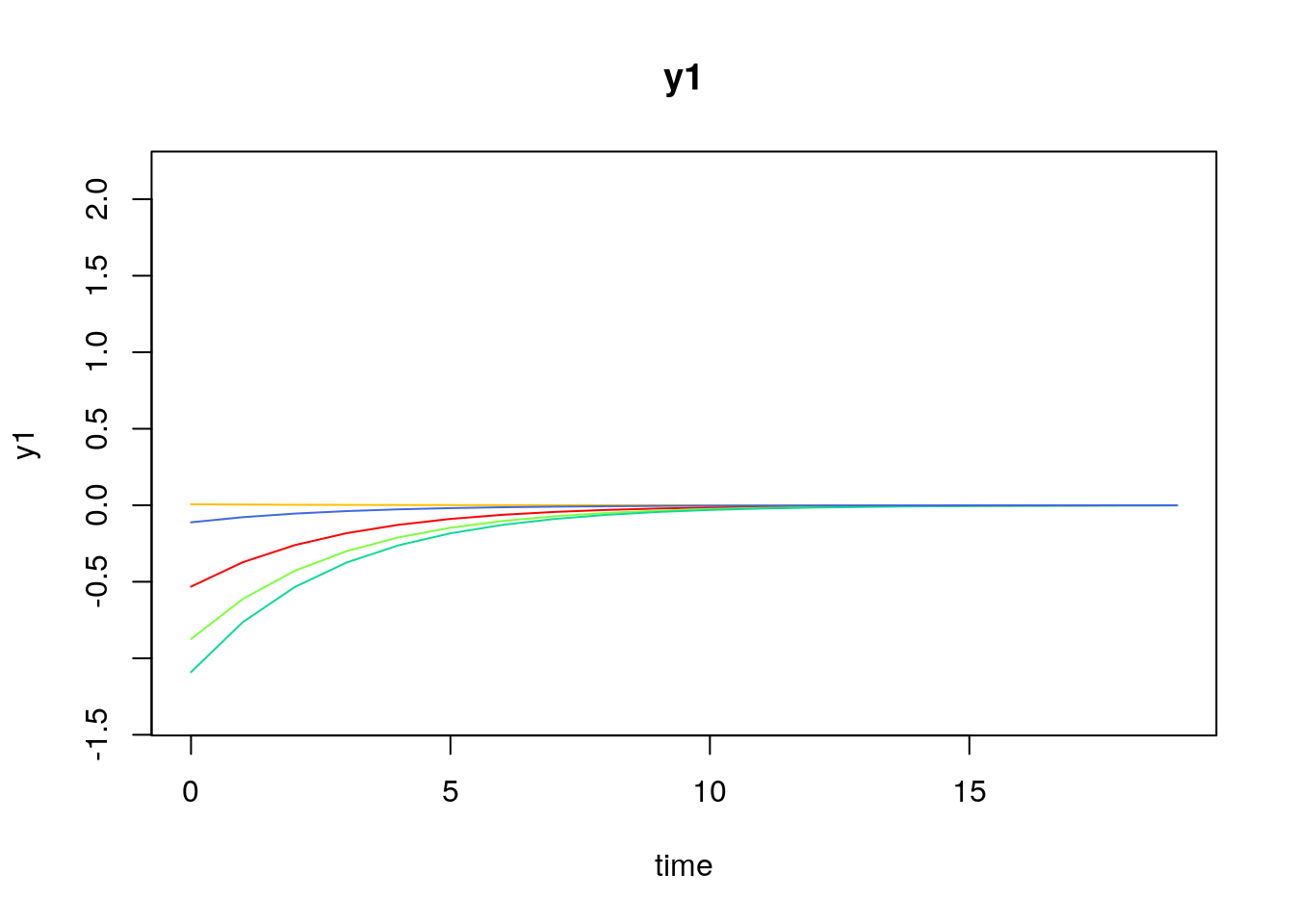
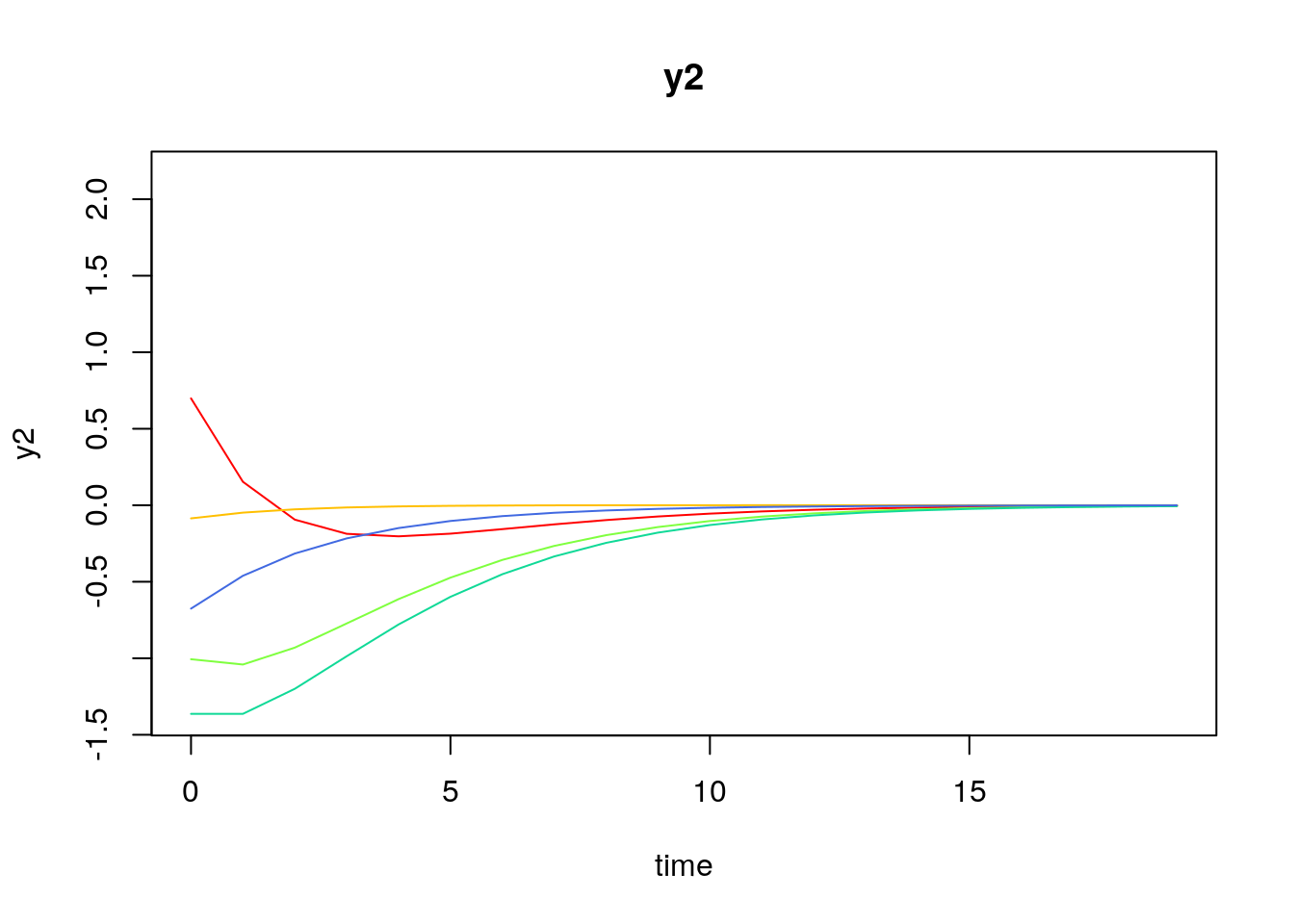
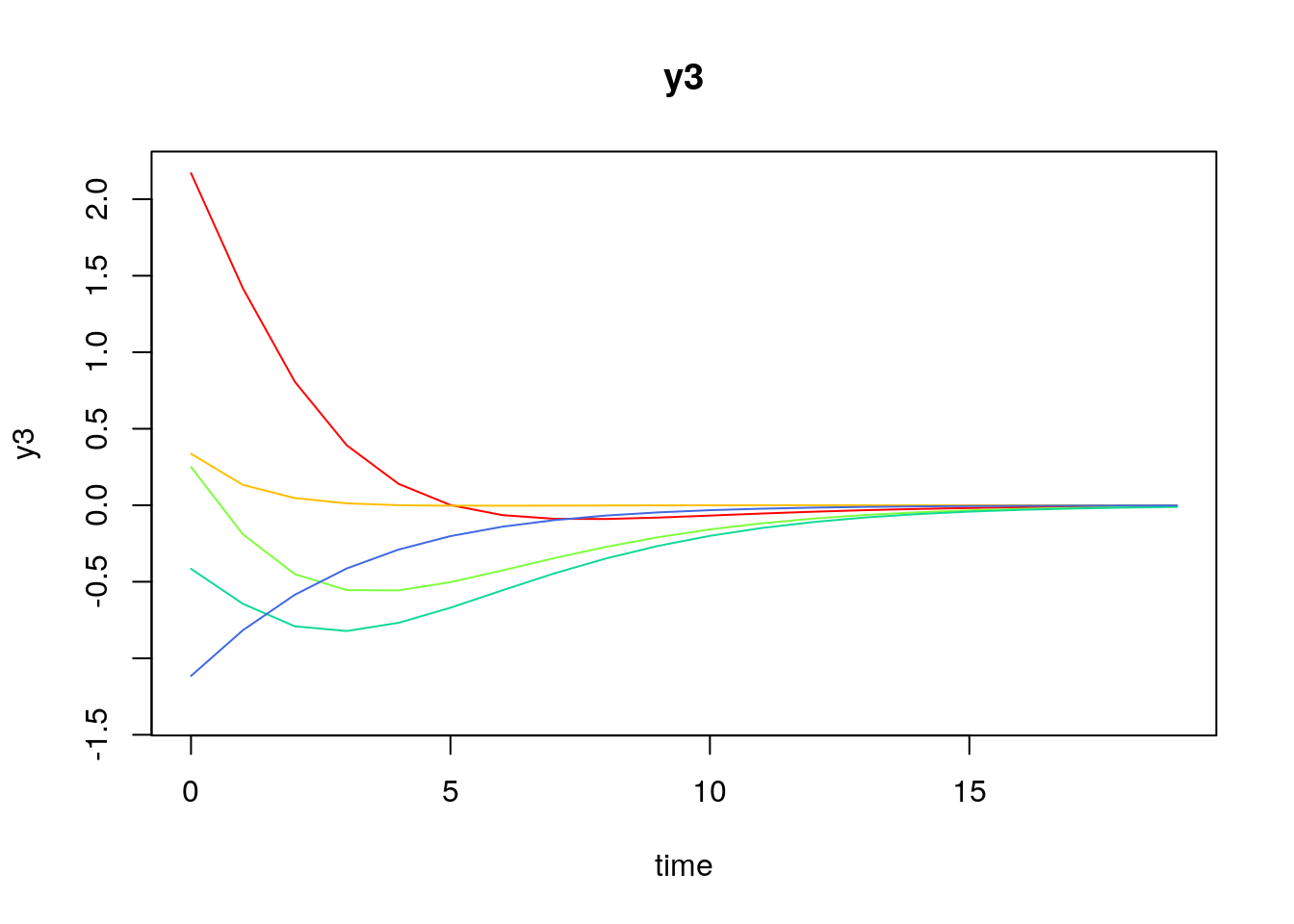
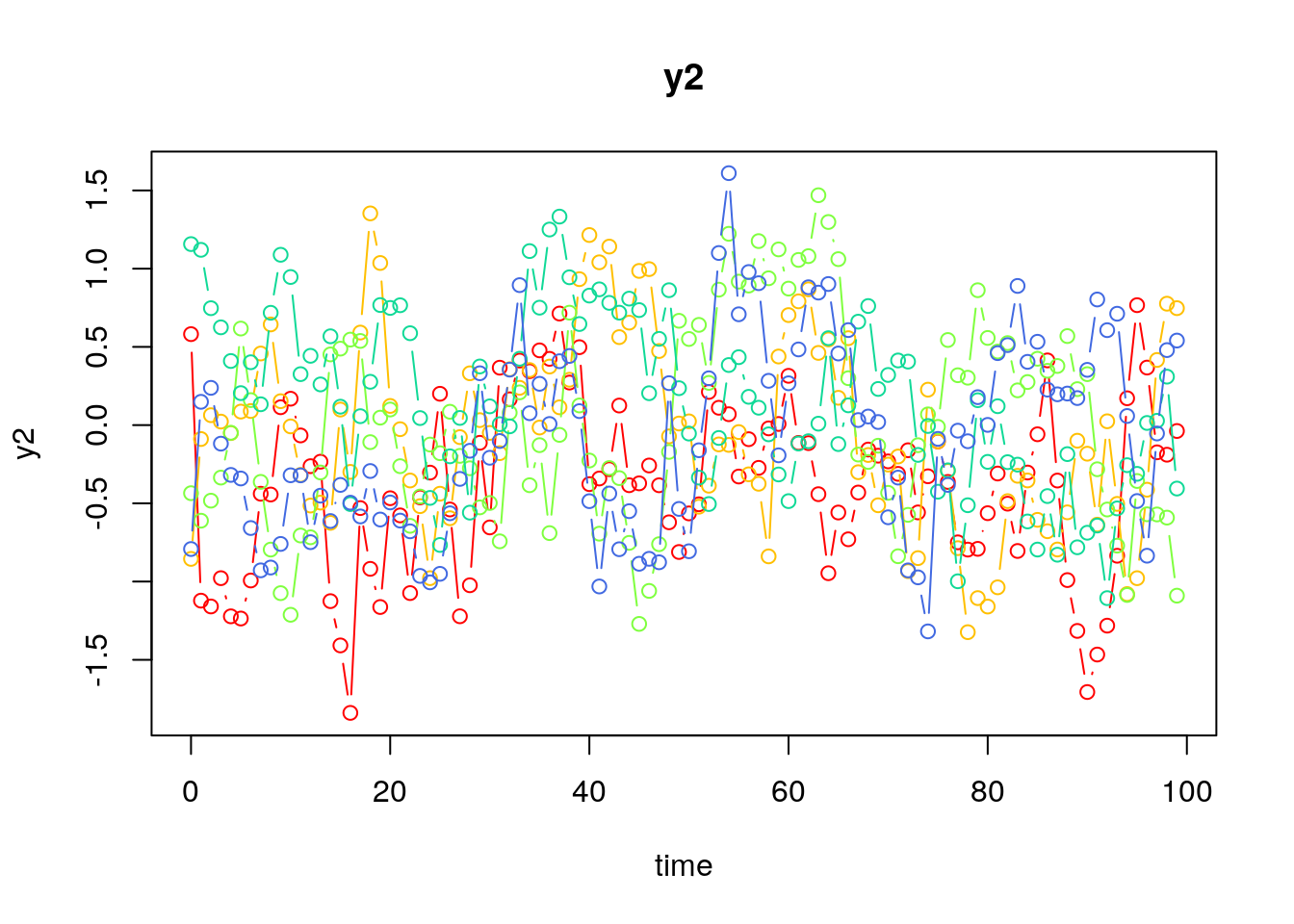
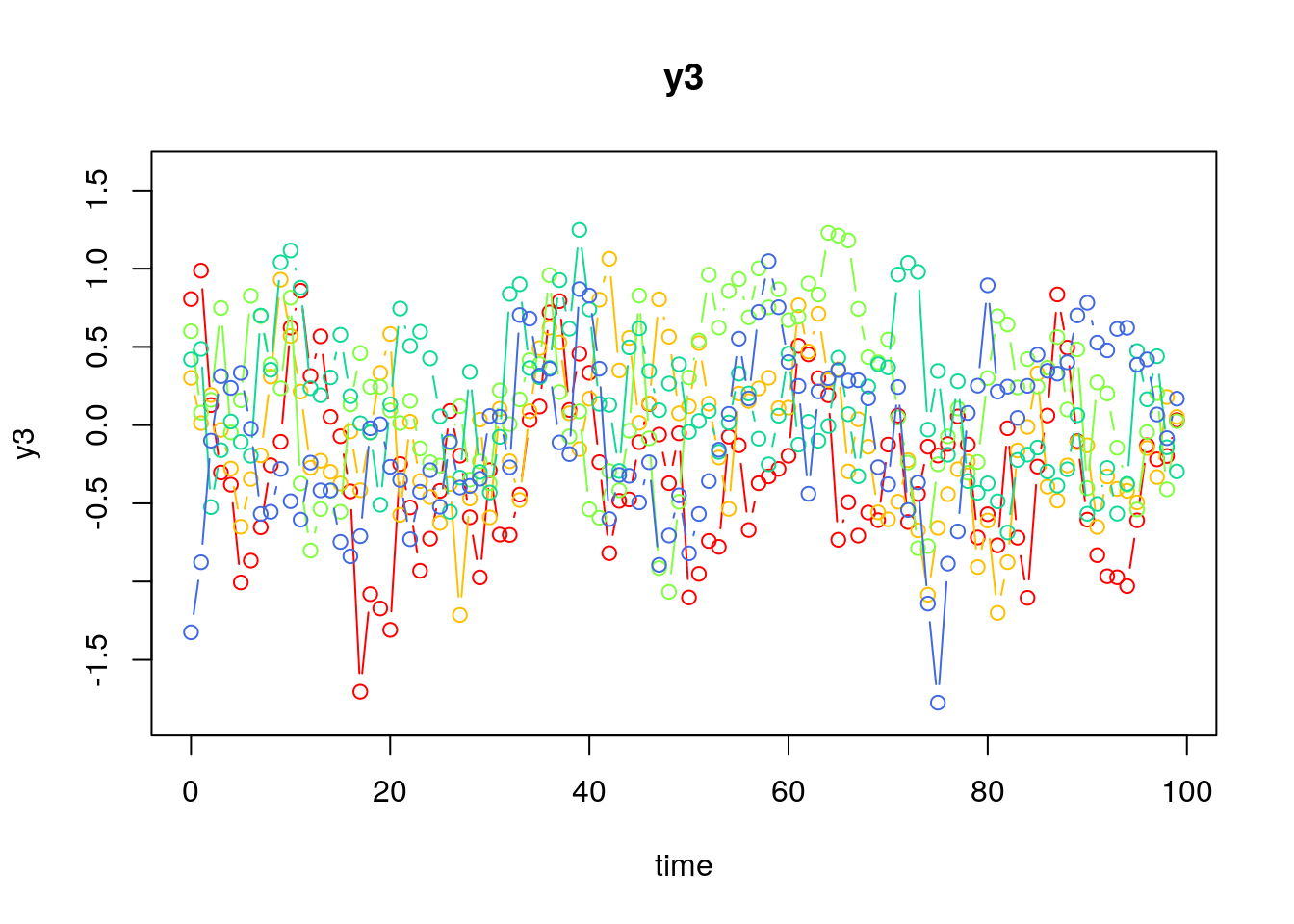
Visualizing the Dynamics Without Process Noise (n = 5 with Different Initial Condition)
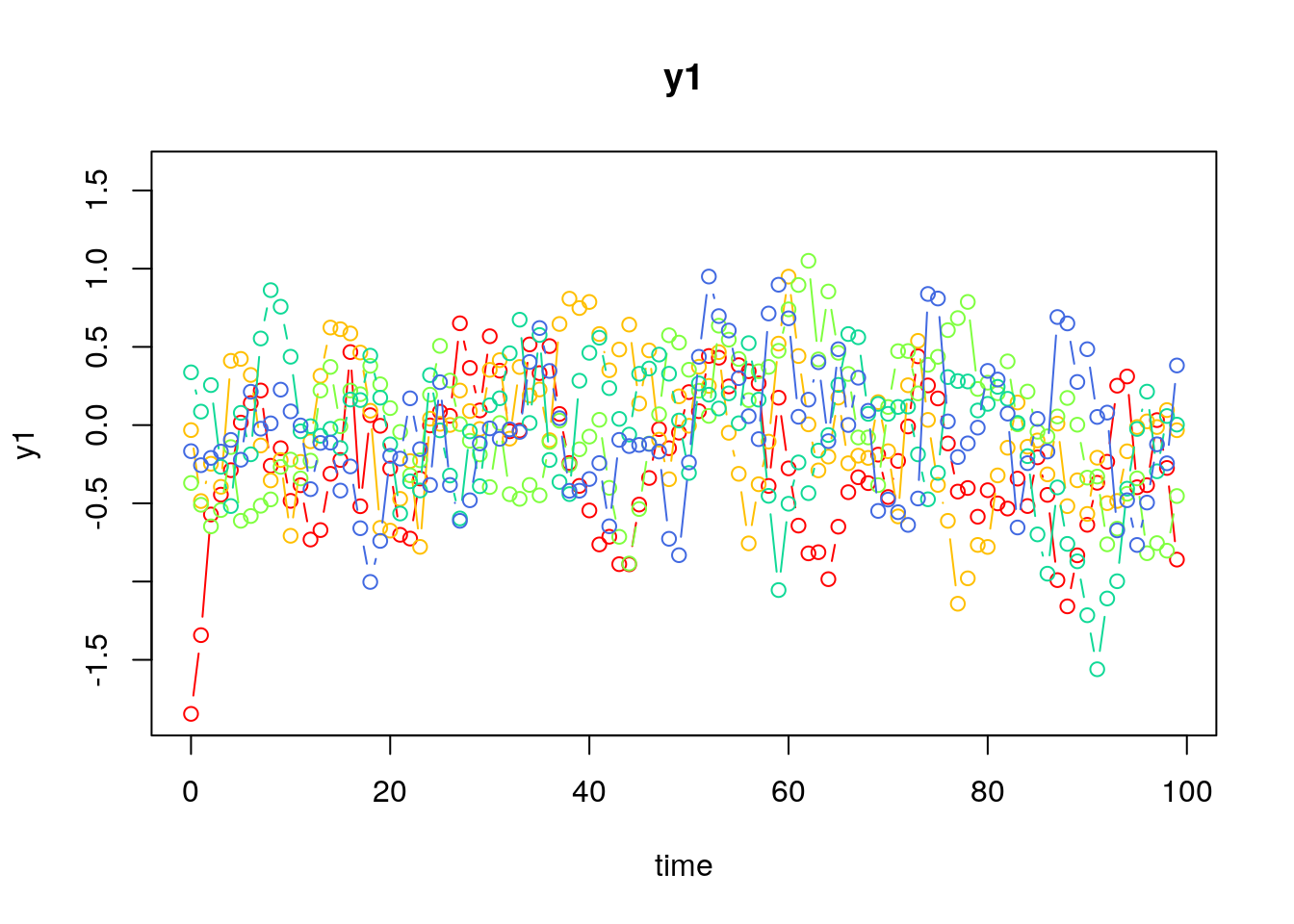
Using the SimSSMVARFixed Function from the simStateSpace Package to Simulate Data
id time y1 y2 y3
1 1 0 -1.84569501 0.5815402 0.8057225
2 1 1 -1.34252674 -1.1219724 0.9873906
3 1 2 -0.57123433 -1.1591679 0.1280274
4 1 3 -0.44448720 -0.9783200 -0.3028425
5 1 4 -0.28796224 -1.2222325 -0.3807219
6 1 5 0.01622801 -1.2362032 -1.0056038
id time y1 y2
Min. :1 Min. : 0.0 Min. :-1.84570 Min. :-2.17817
1st Qu.:2 1st Qu.:249.8 1st Qu.:-0.31071 1st Qu.:-0.42138
Median :3 Median :499.5 Median :-0.01764 Median :-0.01740
Mean :3 Mean :499.5 Mean :-0.01425 Mean :-0.02021
3rd Qu.:4 3rd Qu.:749.2 3rd Qu.: 0.27870 3rd Qu.: 0.37021
Max. :5 Max. :999.0 Max. : 1.56537 Max. : 2.83572
y3
Min. :-1.774215
1st Qu.:-0.363420
Median :-0.005834
Mean :-0.009098
3rd Qu.: 0.341318
Max. : 1.817859
Model Fitting
Prepare Data
dynr_data <- dynr :: dynr.data ( data = data ,
id = "id" ,
time = "time" ,
observed = c ( "y1" , "y2" , "y3" )
)
Prepare Initial Condition
dynr_initial <- dynr :: prep.initial ( values.inistate = mu0 ,
params.inistate = c ( "mu0_1_1" , "mu0_2_1" , "mu0_3_1" ) ,
values.inicov = sigma0 ,
params.inicov = matrix (
data = c (
"sigma0_1_1" , "sigma0_2_1" , "sigma0_3_1" ,
"sigma0_2_1" , "sigma0_2_2" , "sigma0_3_2" ,
"sigma0_3_1" , "sigma0_3_2" , "sigma0_3_3"
) ,
nrow = 3
)
)
Prepare Measurement Model
dynr_measurement <- dynr :: prep.measurement ( values.load = diag ( 3 ) ,
params.load = matrix ( data = "fixed" , nrow = 3 , ncol = 3 ) ,
state.names = c ( "eta_1" , "eta_2" , "eta_3" ) ,
obs.names = c ( "y1" , "y2" , "y3" )
)
Prepare Dynamic Process
dynr_dynamics <- dynr :: prep.formulaDynamics ( formula = list (
eta_1 ~ alpha_1_1 * 1 + beta_1_1 * eta_1 + beta_1_2 * eta_2 + beta_1_3 * eta_3 ,
eta_2 ~ alpha_2_1 * 1 + beta_2_1 * eta_1 + beta_2_2 * eta_2 + beta_2_3 * eta_3 ,
eta_3 ~ alpha_3_1 * 1 + beta_3_1 * eta_1 + beta_3_2 * eta_2 + beta_3_3 * eta_3
) ,
startval = c (
alpha_1_1 = alpha [ 1 ] , alpha_2_1 = alpha [ 2 ] , alpha_3_1 = alpha [ 3 ] ,
beta_1_1 = beta [ 1 , 1 ] , beta_1_2 = beta [ 1 , 2 ] , beta_1_3 = beta [ 1 , 3 ] ,
beta_2_1 = beta [ 2 , 1 ] , beta_2_2 = beta [ 2 , 2 ] , beta_2_3 = beta [ 2 , 3 ] ,
beta_3_1 = beta [ 3 , 1 ] , beta_3_2 = beta [ 3 , 2 ] , beta_3_3 = beta [ 3 , 3 ]
) ,
isContinuousTime = FALSE
)
Prepare Process Noise
dynr_noise <- dynr :: prep.noise ( values.latent = psi ,
params.latent = matrix (
data = c (
"psi_1_1" , "psi_2_1" , "psi_3_1" ,
"psi_2_1" , "psi_2_2" , "psi_3_2" ,
"psi_3_1" , "psi_3_2" , "psi_3_3"
) ,
nrow = 3
) ,
values.observed = matrix ( data = 0 , nrow = 3 , ncol = 3 ) ,
params.observed = matrix ( data = "fixed" , nrow = 3 , ncol = 3 )
)
Prepare the Model
model <- dynr :: dynr.model ( data = dynr_data ,
initial = dynr_initial ,
measurement = dynr_measurement ,
dynamics = dynr_dynamics ,
noise = dynr_noise ,
outfile = "var.c"
)
Fit the Model
results <- dynr :: dynr.cook ( model ,
debug_flag = TRUE ,
verbose = FALSE
)
[1] "Get ready!!!!"
using C compiler: ‘gcc (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’
Optimization function called.
Starting Hessian calculation ...
Finished Hessian calculation.
Original exit flag: 3
Modified exit flag: 3
Optimization terminated successfully: ftol_rel or ftol_abs was reached.
Original fitted parameters: -0.003531293 -0.001280376 0.001523566 0.6895684
0.01390681 -0.003940273 0.4892806 0.6166874 -0.00850994 -0.1131785 0.4157686
0.4948645 -2.314722 -0.02295081 -0.01630225 -2.301541 -0.01437825 -2.302993
-0.7217189 0.5433516 0.8634073 -0.2858639 -1.244706 0.1022364 0.00547225
0.08818863 -1.187881
Transformed fitted parameters: -0.003531293 -0.001280376 0.001523566 0.6895684
0.01390681 -0.003940273 0.4892806 0.6166874 -0.00850994 -0.1131785 0.4157686
0.4948645 0.09879361 -0.002267393 -0.001610558 0.1001565 -0.001402363 0.1000062
-0.7217189 0.5433516 0.8634073 0.7513649 -0.9352283 0.07681685 2.169571
-0.006941846 0.3205399
Doing end processing
Successful trial
Total Time: 2.207808
Backend Time: 2.200906
Summary
Coefficients:
Estimate Std. Error t value ci.lower ci.upper Pr(>|t|)
alpha_1_1 -0.0035313 0.0044508 -0.793 -0.0122548 0.0051922 0.2138
alpha_2_1 -0.0012804 0.0044814 -0.286 -0.0100638 0.0075031 0.3876
alpha_3_1 0.0015236 0.0044781 0.340 -0.0072533 0.0103004 0.3668
beta_1_1 0.6895684 0.0112672 61.202 0.6674852 0.7116517 <2e-16 ***
beta_1_2 0.0139068 0.0093820 1.482 -0.0044815 0.0322952 0.0692 .
beta_1_3 -0.0039403 0.0095679 -0.412 -0.0226930 0.0148125 0.3402
beta_2_1 0.4892806 0.0113446 43.129 0.4670456 0.5115157 <2e-16 ***
beta_2_2 0.6166874 0.0094464 65.283 0.5981727 0.6352020 <2e-16 ***
beta_2_3 -0.0085099 0.0096336 -0.883 -0.0273915 0.0103716 0.1885
beta_3_1 -0.1131785 0.0113361 -9.984 -0.1353969 -0.0909601 <2e-16 ***
beta_3_2 0.4157686 0.0094393 44.047 0.3972680 0.4342693 <2e-16 ***
beta_3_3 0.4948645 0.0096263 51.408 0.4759973 0.5137317 <2e-16 ***
psi_1_1 0.0987936 0.0019768 49.976 0.0949191 0.1026681 <2e-16 ***
psi_2_1 -0.0022674 0.0014078 -1.611 -0.0050266 0.0004919 0.0537 .
psi_3_1 -0.0016106 0.0014066 -1.145 -0.0043674 0.0011463 0.1261
psi_2_2 0.1001565 0.0020041 49.975 0.0962285 0.1040845 <2e-16 ***
psi_3_2 -0.0014024 0.0014162 -0.990 -0.0041780 0.0013733 0.1611
psi_3_3 0.1000062 0.0020011 49.976 0.0960841 0.1039282 <2e-16 ***
mu0_1_1 -0.7217189 0.3854554 -1.872 -1.4771977 0.0337599 0.0306 *
mu0_2_1 0.5433516 0.6542311 0.831 -0.7389178 1.8256210 0.2031
mu0_3_1 0.8634073 0.2531618 3.410 0.3672192 1.3595954 0.0003 ***
sigma0_1_1 0.7513649 0.4740246 1.585 -0.1777063 1.6804360 0.0565 .
sigma0_2_1 -0.9352283 0.7049527 -1.327 -2.3169103 0.4464537 0.0923 .
sigma0_3_1 0.0768168 0.2221450 0.346 -0.3585794 0.5122131 0.3648
sigma0_2_2 2.1695715 1.3671181 1.587 -0.5099307 4.8490737 0.0563 .
sigma0_3_2 -0.0069418 0.3726743 -0.019 -0.7373700 0.7234863 0.4926
sigma0_3_3 0.3205399 0.2023250 1.584 -0.0760099 0.7170897 0.0566 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
-2 log-likelihood value at convergence = 8000.08
AIC = 8054.08
BIC = 8230.05
Parameter Estimates
[1] -0.003531293 -0.001280376 0.001523566
[,1] [,2] [,3]
[1,] 0.6895684 0.01390681 -0.003940273
[2,] 0.4892806 0.61668735 -0.008509940
[3,] -0.1131785 0.41576863 0.494864534
[,1] [,2] [,3]
[1,] 0.098793608 -0.002267393 -0.001610558
[2,] -0.002267393 0.100156481 -0.001402363
[3,] -0.001610558 -0.001402363 0.100006157
[1] -0.7217189 0.5433516 0.8634073
[,1] [,2] [,3]
[1,] 0.75136488 -0.935228319 0.076816849
[2,] -0.93522832 2.169571479 -0.006941846
[3,] 0.07681685 -0.006941846 0.320539871