The Vector Autoregressive Model

Ivan Jacob Agaloos Pesigan

2026-01-04

Model

The measurement model is given by $$\begin{equation} \mathbf{y}_{i, t} = \boldsymbol{\eta}_{i, t} \end{equation}$$ where $\mathbf{y}_{i, t}$ represents a vector of observed variables and $\boldsymbol{\eta}_{i, t}$ a vector of latent variables for individual $i$ and time $t$. Since the observed and latent variables are equal, we only generate data from the dynamic structure.

The dynamic structure is given by $$\begin{equation} \boldsymbol{\eta}_{i, t} = \boldsymbol{\alpha} + \boldsymbol{\beta} \boldsymbol{\eta}_{i, t - 1} + \boldsymbol{\zeta}_{i, t}, \quad \mathrm{with} \quad \boldsymbol{\zeta}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \boldsymbol{\Psi} \right) \end{equation}$$ where $\boldsymbol{\eta}_{i, t}$, $\boldsymbol{\eta}_{i, t - 1}$, and $\boldsymbol{\zeta}_{i, t}$ are random variables, and $\boldsymbol{\alpha}$, $\boldsymbol{\beta}$, and $\boldsymbol{\Psi}$ are model parameters. Here, $\boldsymbol{\eta}_{i, t}$ is a vector of latent variables at time $t$ and individual $i$, $\boldsymbol{\eta}_{i, t - 1}$ represents a vector of latent variables at time $t - 1$ and individual $i$, and $\boldsymbol{\zeta}_{i, t}$ represents a vector of dynamic noise at time $t$ and individual $i$. $\boldsymbol{\alpha}$ denotes a vector of intercepts, $\boldsymbol{\beta}$ a matrix of autoregression and cross regression coefficients, and $\boldsymbol{\Psi}$ the covariance matrix of $\boldsymbol{\zeta}_{i, t}$.

An alternative representation of the dynamic noise is given by $$\begin{equation} \boldsymbol{\zeta}_{i, t} = \boldsymbol{\Psi}^{\frac{1}{2}} \mathbf{z}_{i, t}, \quad \mathrm{with} \quad \mathbf{z}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \mathbf{I} \right) \end{equation}$$ where $\left( \boldsymbol{\Psi}^{\frac{1}{2}} \right) \left( \boldsymbol{\Psi}^{\frac{1}{2}} \right)^{\prime} = \boldsymbol{\Psi}$ .

Data Generation

Notation

Let $t = 1000$ be the number of time points and $n = 100$ be the number of individuals.

Let the initial condition $\boldsymbol{\eta}_{0}$ be given by

$$\begin{equation} \boldsymbol{\eta}_{0} \sim \mathcal{N} \left( \boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}, \boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0} \right) \end{equation}$$

$$\begin{equation} \boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0} = \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right) \end{equation}$$

$$\begin{equation} \boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0} = \left( \begin{array}{ccc} 0.1960784 & 0.1183232 & 0.0298539 \\ 0.1183232 & 0.3437711 & 0.1381855 \\ 0.0298539 & 0.1381855 & 0.2663828 \\ \end{array} \right) . \end{equation}$$

Let the constant vector $\boldsymbol{\alpha}$ be given by

$$\begin{equation} \boldsymbol{\alpha} = \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right) . \end{equation}$$

Let the transition matrix $\boldsymbol{\beta}$ be given by

$$\begin{equation} \boldsymbol{\beta} = \left( \begin{array}{ccc} 0.7 & 0 & 0 \\ 0.5 & 0.6 & 0 \\ -0.1 & 0.4 & 0.5 \\ \end{array} \right) . \end{equation}$$

Let the dynamic process noise $\boldsymbol{\Psi}$ be given by

$$\begin{equation} \boldsymbol{\Psi} = \left( \begin{array}{ccc} 0.1 & 0 & 0 \\ 0 & 0.1 & 0 \\ 0 & 0 & 0.1 \\ \end{array} \right) . \end{equation}$$

R Function Arguments

n
#> [1] 100
time
#> [1] 1000
mu0
#> [1] 0 0 0
sigma0
#>            [,1]      [,2]       [,3]
#> [1,] 0.19607843 0.1183232 0.02985385
#> [2,] 0.11832319 0.3437711 0.13818551
#> [3,] 0.02985385 0.1381855 0.26638284
sigma0_l # sigma0_l <- t(chol(sigma0))
#>            [,1]      [,2]     [,3]
#> [1,] 0.44280744 0.0000000 0.000000
#> [2,] 0.26721139 0.5218900 0.000000
#> [3,] 0.06741949 0.2302597 0.456966
alpha
#> [1] 0 0 0
beta
#>      [,1] [,2] [,3]
#> [1,]  0.7  0.0  0.0
#> [2,]  0.5  0.6  0.0
#> [3,] -0.1  0.4  0.5
psi
#>      [,1] [,2] [,3]
#> [1,]  0.1  0.0  0.0
#> [2,]  0.0  0.1  0.0
#> [3,]  0.0  0.0  0.1
psi_l # psi_l <- t(chol(psi))
#>           [,1]      [,2]      [,3]
#> [1,] 0.3162278 0.0000000 0.0000000
#> [2,] 0.0000000 0.3162278 0.0000000
#> [3,] 0.0000000 0.0000000 0.3162278

Visualizing the Dynamics Without Process Noise (n = 5 with Different Initial Condition)

Using the SimSSMVARFixed Function from the simStateSpace Package to Simulate Data

library(simStateSpace)
sim <- SimSSMVARFixed(
  n = n,
  time = time,
  mu0 = mu0,
  sigma0_l = sigma0_l,
  alpha = alpha,
  beta = beta,
  psi_l = psi_l
)
data <- as.data.frame(sim)
head(data)
#>   id time          y1          y2          y3
#> 1  1    0 -0.81728749  0.01319023  0.57975035
#> 2  1    1 -0.62264147 -0.94877859  0.54422379
#> 3  1    2 -0.06731464 -0.69530903 -0.09626706
#> 4  1    3 -0.09174342 -0.44804477 -0.27983813
#> 5  1    4 -0.04104160 -0.72769549 -0.19238403
#> 6  1    5  0.18907246 -0.81602072 -0.73831208
summary(data)
#>        id              time             y1                   y2            
#>  Min.   :  1.00   Min.   :  0.0   Min.   :-1.9239387   Min.   :-2.6896682  
#>  1st Qu.: 25.75   1st Qu.:249.8   1st Qu.:-0.2991519   1st Qu.:-0.3940385  
#>  Median : 50.50   Median :499.5   Median :-0.0029441   Median : 0.0008316  
#>  Mean   : 50.50   Mean   :499.5   Mean   :-0.0005164   Mean   : 0.0004548  
#>  3rd Qu.: 75.25   3rd Qu.:749.2   3rd Qu.: 0.2957664   3rd Qu.: 0.3976987  
#>  Max.   :100.00   Max.   :999.0   Max.   : 1.9753039   Max.   : 2.3189032  
#>        y3           
#>  Min.   :-2.185100  
#>  1st Qu.:-0.343439  
#>  Median : 0.001899  
#>  Mean   : 0.002713  
#>  3rd Qu.: 0.351819  
#>  Max.   : 2.113439
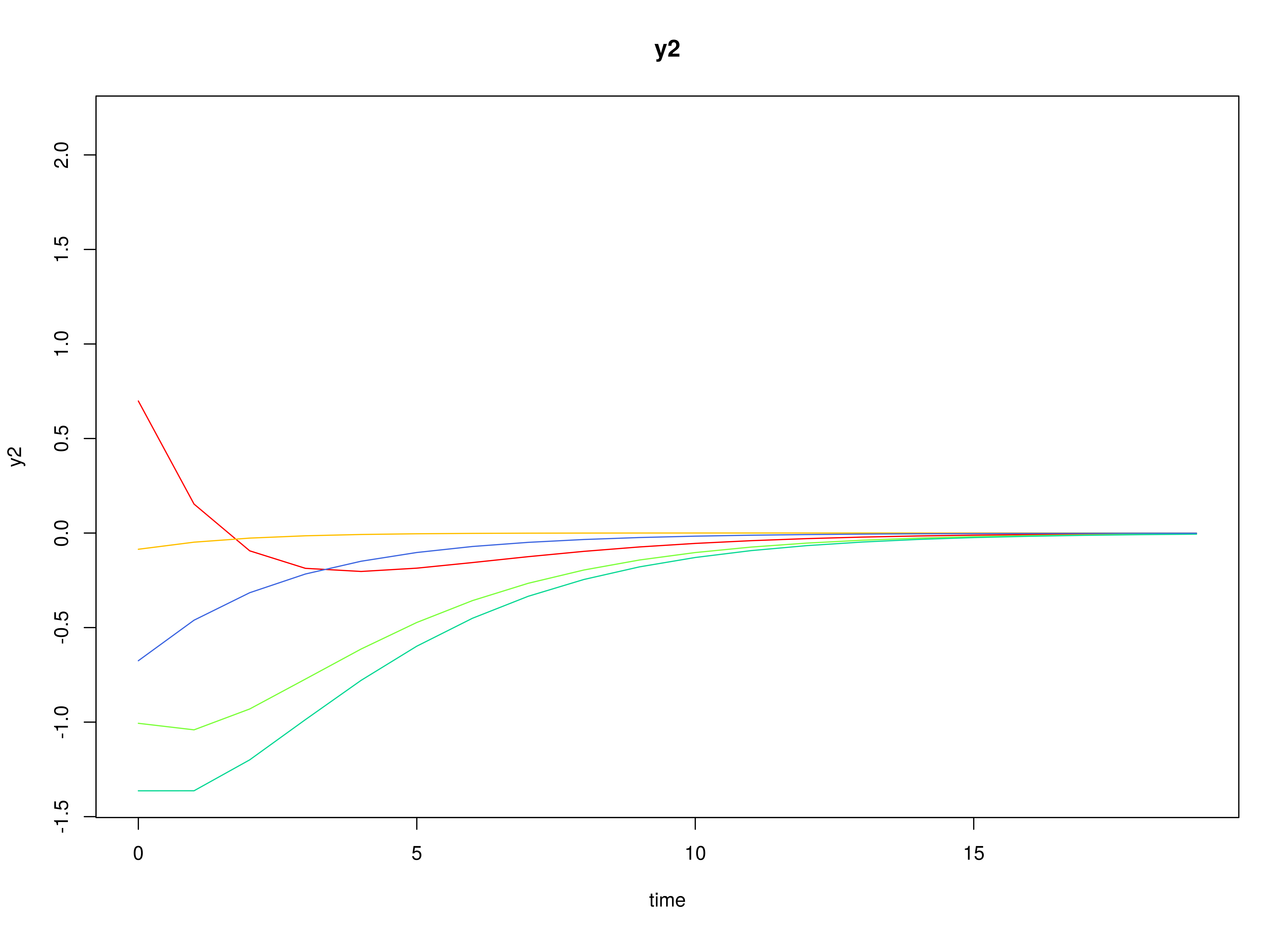
plot(sim)

Model Fitting

Prepare Data

dynr_data <- dynr::dynr.data(
  data = data,
  id = "id",
  time = "time",
  observed = c("y1", "y2", "y3")
)

Prepare Initial Condition

dynr_initial <- dynr::prep.initial(
  values.inistate = mu0,
  params.inistate = c("mu0_1_1", "mu0_2_1", "mu0_3_1"),
  values.inicov = sigma0,
  params.inicov = matrix(
    data = c(
      "sigma0_1_1", "sigma0_2_1", "sigma0_3_1",
      "sigma0_2_1", "sigma0_2_2", "sigma0_3_2",
      "sigma0_3_1", "sigma0_3_2", "sigma0_3_3"
    ),
    nrow = 3
  )
)

Prepare Measurement Model

dynr_measurement <- dynr::prep.measurement(
  values.load = diag(3),
  params.load = matrix(data = "fixed", nrow = 3, ncol = 3),
  state.names = c("eta_1", "eta_2", "eta_3"),
  obs.names = c("y1", "y2", "y3")
)

Prepare Dynamic Process

dynr_dynamics <- dynr::prep.formulaDynamics(
  formula = list(
    eta_1 ~ alpha_1_1 * 1 + beta_1_1 * eta_1 + beta_1_2 * eta_2 + beta_1_3 * eta_3,
    eta_2 ~ alpha_2_1 * 1 + beta_2_1 * eta_1 + beta_2_2 * eta_2 + beta_2_3 * eta_3,
    eta_3 ~ alpha_3_1 * 1 + beta_3_1 * eta_1 + beta_3_2 * eta_2 + beta_3_3 * eta_3
  ),
  startval = c(
    alpha_1_1 = alpha[1], alpha_2_1 = alpha[2], alpha_3_1 = alpha[3],
    beta_1_1 = beta[1, 1], beta_1_2 = beta[1, 2], beta_1_3 = beta[1, 3],
    beta_2_1 = beta[2, 1], beta_2_2 = beta[2, 2], beta_2_3 = beta[2, 3],
    beta_3_1 = beta[3, 1], beta_3_2 = beta[3, 2], beta_3_3 = beta[3, 3]
  ),
  isContinuousTime = FALSE
)

Prepare Process Noise

dynr_noise <- dynr::prep.noise(
  values.latent = psi,
  params.latent = matrix(
    data = c(
      "psi_1_1", "psi_2_1", "psi_3_1",
      "psi_2_1", "psi_2_2", "psi_3_2",
      "psi_3_1", "psi_3_2", "psi_3_3"
    ),
    nrow = 3
  ),
  values.observed = matrix(data = 0, nrow = 3, ncol = 3),
  params.observed = matrix(data = "fixed", nrow = 3, ncol = 3)
)

Prepare the Model

model <- dynr::dynr.model(
  data = dynr_data,
  initial = dynr_initial,
  measurement = dynr_measurement,
  dynamics = dynr_dynamics,
  noise = dynr_noise,
  outfile = "var.c"
)

Fit the Model

results <- dynr::dynr.cook(
  model,
  debug_flag = TRUE,
  verbose = FALSE
)
#> [1] "Get ready!!!!"
#> using C compiler: ‘gcc (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’
#> Optimization function called.
#> Starting Hessian calculation ...
#> Finished Hessian calculation.
#> Original exit flag:  3 
#> Modified exit flag:  3 
#> Optimization terminated successfully: ftol_rel or ftol_abs was reached. 
#> Original fitted parameters:  -0.0002106191 0.0002611953 0.0009243711 0.6972055 
#> 0.0006123363 0.002917173 0.4995238 0.6005427 -0.001770816 -0.1015684 0.4031293 
#> 0.4972227 -2.301822 -0.003746232 0.001270917 -2.306638 0.002932051 -2.304454 
#> -0.03405394 0.08081097 0.1345955 -1.449063 0.6212102 0.02495321 -1.163541 
#> 0.3906056 -1.540209 
#> 
#> Transformed fitted parameters:  -0.0002106191 0.0002611953 0.0009243711 
#> 0.6972055 0.0006123363 0.002917173 0.4995238 0.6005427 -0.001770816 -0.1015684 
#> 0.4031293 0.4972227 0.1000764 -0.0003749093 0.0001271887 0.09959695 
#> 0.0002915427 0.09981433 -0.03405394 0.08081097 0.1345955 0.2347902 0.1458541 
#> 0.005858769 0.4029841 0.1256562 0.2621428 
#> 
#> Doing end processing
#> Successful trial
#> Total Time: 1.395497 
#> Backend Time: 1.395319

Summary

summary(results)
#> Coefficients:
#>              Estimate Std. Error t value   ci.lower   ci.upper Pr(>|t|)    
#> alpha_1_1  -0.0002106  0.0010009  -0.210 -0.0021723  0.0017511   0.4167    
#> alpha_2_1   0.0002612  0.0009985   0.262 -0.0016958  0.0022182   0.3968    
#> alpha_3_1   0.0009244  0.0009996   0.925 -0.0010348  0.0028835   0.1775    
#> beta_1_1    0.6972055  0.0025524 273.155  0.6922029  0.7022082   <2e-16 ***
#> beta_1_2    0.0006123  0.0021518   0.285 -0.0036052  0.0048299   0.3880    
#> beta_1_3    0.0029172  0.0021943   1.329 -0.0013836  0.0072179   0.0919 .  
#> beta_2_1    0.4995238  0.0025463 196.178  0.4945332  0.5045144   <2e-16 ***
#> beta_2_2    0.6005427  0.0021466 279.766  0.5963354  0.6047499   <2e-16 ***
#> beta_2_3   -0.0017708  0.0021890  -0.809 -0.0060612  0.0025196   0.2093    
#> beta_3_1   -0.1015684  0.0025490 -39.847 -0.1065643 -0.0965726   <2e-16 ***
#> beta_3_2    0.4031293  0.0021491 187.579  0.3989171  0.4073415   <2e-16 ***
#> beta_3_3    0.4972227  0.0021915 226.886  0.4929274  0.5015180   <2e-16 ***
#> psi_1_1     0.1000764  0.0004478 223.500  0.0991988  0.1009540   <2e-16 ***
#> psi_2_1    -0.0003749  0.0003159  -1.187 -0.0009940  0.0002442   0.1176    
#> psi_3_1     0.0001272  0.0003162   0.402 -0.0004925  0.0007469   0.3438    
#> psi_2_2     0.0995969  0.0004456 223.505  0.0987236  0.1004703   <2e-16 ***
#> psi_3_2     0.0002915  0.0003155   0.924 -0.0003267  0.0009098   0.1777    
#> psi_3_3     0.0998143  0.0004466 223.505  0.0989390  0.1006896   <2e-16 ***
#> mu0_1_1    -0.0340539  0.0484227  -0.703 -0.1289606  0.0608527   0.2409    
#> mu0_2_1     0.0808110  0.0634708   1.273 -0.0435895  0.2052114   0.1015    
#> mu0_3_1     0.1345955  0.0511737   2.630  0.0342970  0.2348940   0.0043 ** 
#> sigma0_1_1  0.2347902  0.0330964   7.094  0.1699225  0.2996580   <2e-16 ***
#> sigma0_2_1  0.1458541  0.0340257   4.287  0.0791650  0.2125432   <2e-16 ***
#> sigma0_3_1  0.0058588  0.0247317   0.237 -0.0426146  0.0543321   0.4064    
#> sigma0_2_2  0.4029841  0.0570886   7.059  0.2910926  0.5148757   <2e-16 ***
#> sigma0_3_2  0.1256562  0.0348837   3.602  0.0572854  0.1940269   0.0002 ***
#> sigma0_3_3  0.2621428  0.0369885   7.087  0.1896467  0.3346388   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> -2 log-likelihood value at convergence = 160369.89
#> AIC = 160423.89
#> BIC = 160680.73

Parameter Estimates

alpha_hat
#> [1] -0.0002106191  0.0002611953  0.0009243711
beta_hat
#>            [,1]         [,2]         [,3]
#> [1,]  0.6972055 0.0006123363  0.002917173
#> [2,]  0.4995238 0.6005426823 -0.001770816
#> [3,] -0.1015684 0.4031292921  0.497222703
psi_hat
#>               [,1]          [,2]         [,3]
#> [1,]  0.1000763734 -0.0003749093 0.0001271887
#> [2,] -0.0003749093  0.0995969478 0.0002915427
#> [3,]  0.0001271887  0.0002915427 0.0998143323
mu0_hat
#> [1] -0.03405394  0.08081097  0.13459548
sigma0_hat
#>             [,1]      [,2]        [,3]
#> [1,] 0.234790236 0.1458541 0.005858769
#> [2,] 0.145854079 0.4029841 0.125656157
#> [3,] 0.005858769 0.1256562 0.262142772

References

Chow, S.-M., Ho, M. R., Hamaker, E. L., & Dolan, C. V. (2010). Equivalence and differences between structural equation modeling and state-space modeling techniques. Structural Equation Modeling: A Multidisciplinary Journal, 17(2), 303–332. https://doi.org/10.1080/10705511003661553

Ou, L., Hunter, M. D., & Chow, S.-M. (2019). What’s for dynr: A package for linear and nonlinear dynamic modeling in R. The R Journal, 11(1), 91. https://doi.org/10.32614/rj-2019-012

Pesigan, I. J. A., Russell, M. A., & Chow, S.-M. (2025). Inferences and effect sizes for direct, indirect, and total effects in continuous-time mediation models. Psychological Methods. https://doi.org/10.1037/met0000779

R Core Team. (2025). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/