Skip to contents

MCStd Function Use Case 4: Difference of Standardized Regression Coefficients in Multiple Groups

Ivan Jacob Agaloos Pesigan

2024-04-14

Source: vignettes/mcstd-4-difference-regression-coefficients-multigroup.Rmd
mcstd-4-difference-regression-coefficients-multigroup.Rmd

The MCStd() function is used to generate Monte Carlo confidence intervals for differences between standardized regression coefficients in multiple groups.

Data

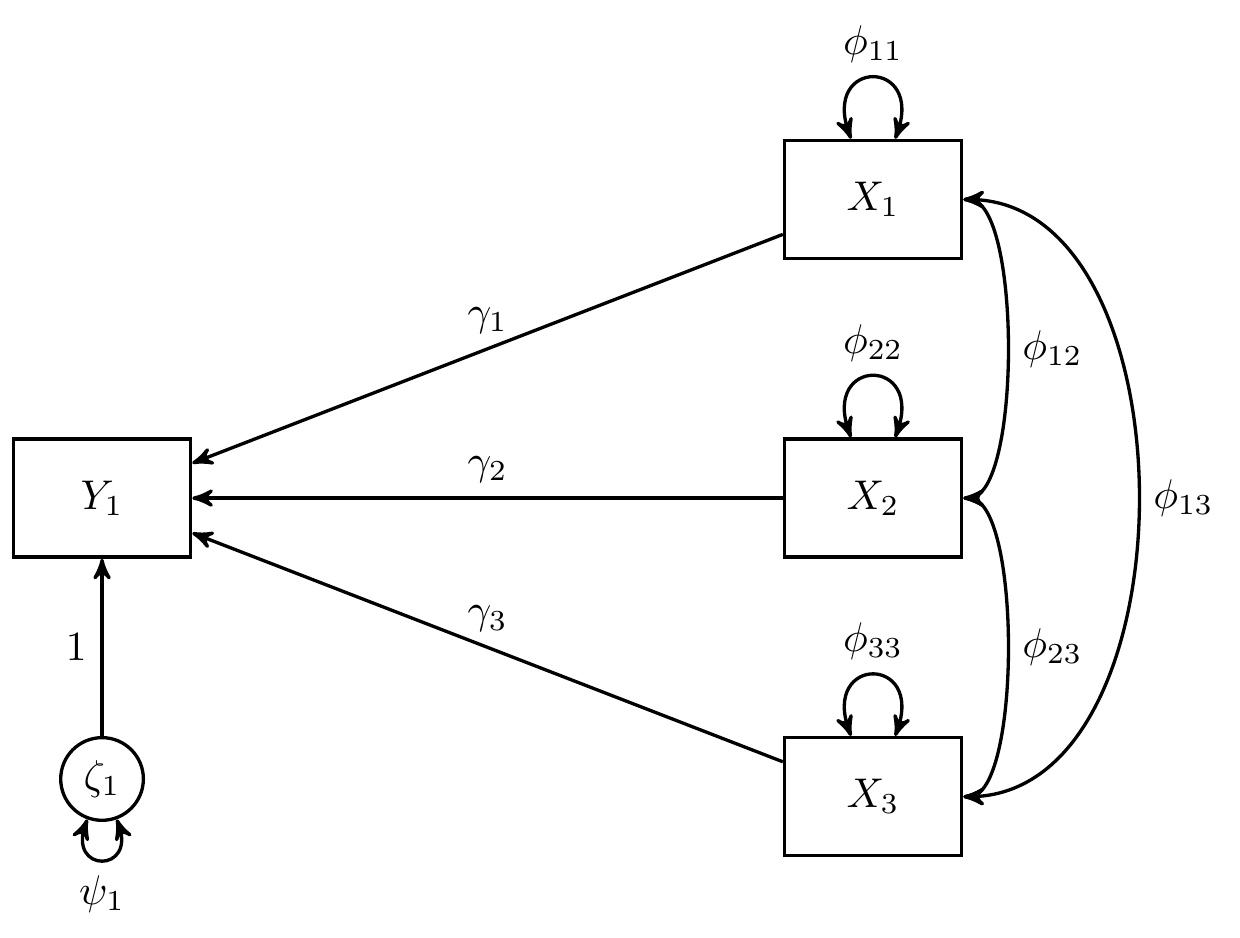
In this example, we use data from Kwan & Chan (2014) with three groups (Hong Kong, Japan, and Korea) where child’s reading ability (\(Y_{1}\)) is regressed on parental occupational status (\(X_{1}\)), parental educational level (\(X_{2}\)), and child’s home possession (\(X_{3}\))

\[ Y_{1} = \alpha_{1} + \gamma_{1} X_{1} + \gamma_{2} X_{2} + \gamma_{3} X_{3} + \zeta_{1} . \]

Note that \(\zeta_{1}\) is the stochastic error term with expected value of zero and finite variance \(\psi_{1}\), \(\alpha_{1}\) is the intercept, and \(\gamma_{1}\), \(\gamma_{2}\), and \(\gamma_{3}\) are regression coefficients.

A Three-Regressor Multiple Regression Model (Covariance Structure)
A Three-Regressor Multiple Regression Model (Covariance Structure)
knitr::kable(
  x = covs_hongkong, digits = 4,
  caption = "Covariance Matrix for Hong Kong"
)
Covariance Matrix for Hong Kong
Y1 X1 X2 X3
Y1 8176.0021 27.3990 28.2320 31.2722
X1 27.3990 0.9451 0.6006 0.4326
X2 28.2320 0.6006 0.7977 0.3779
X3 31.2722 0.4326 0.3779 0.8956 
nobs_hongkong
#> [1] 4625
knitr::kable(
  x = covs_japan, digits = 4,
  caption = "Covariance Matrix for Japan"
)
Covariance Matrix for Japan
Y1 X1 X2 X3
Y1 9666.8658 34.2501 35.2189 30.6472
X1 34.2501 1.0453 0.6926 0.5027
X2 35.2189 0.6926 1.0777 0.4524
X3 30.6472 0.5027 0.4524 0.9583 
nobs_japan
#> [1] 5943
knitr::kable(
  x = covs_korea, digits = 4,
  caption = "Covariance Matrix for Korea"
)
Covariance Matrix for Korea
Y1 X1 X2 X3
Y1 8187.6921 31.6266 37.3062 30.9021
X1 31.6266 0.9271 0.6338 0.4088
X2 37.3062 0.6338 1.0007 0.3902
X3 30.9021 0.4088 0.3902 0.8031 
nobs_korea
#> [1] 5151

Model Specification

We regress Y1 on X1, X2, and X3. We label the regression coefficient \(\gamma_{1}\) for the three groups as gamma1.g1, gamma1.g2, and gamma1.g3, \(\gamma_{2}\) for the three groups as gamma2.g1, gamma2.g2, and gamma2.g3, and \(\gamma_{3}\) for the three groups as gamma3.g1, gamma3.g2, and gamma3.g3.

model <- "
  Y1 ~ c(gamma1.g1, gamma1.g2, gamma1.g3) * X1
  Y1 ~ c(gamma2.g1, gamma2.g2, gamma2.g3) * X2
  Y1 ~ c(gamma3.g1, gamma3.g2, gamma3.g3) * X3
  gamma1.g12 := gamma1.g1 - gamma1.g2
  gamma1.g13 := gamma1.g1 - gamma1.g3
  gamma1.g23 := gamma1.g2 - gamma1.g3
  gamma2.g12 := gamma2.g1 - gamma2.g2
  gamma2.g13 := gamma2.g1 - gamma2.g3
  gamma2.g23 := gamma2.g2 - gamma2.g3
  gamma3.g12 := gamma3.g1 - gamma3.g2
  gamma3.g13 := gamma3.g1 - gamma3.g3
  gamma3.g23 := gamma3.g2 - gamma3.g3
"

Model Fitting

We can now fit the model using the sem() function from lavaan with mimic = "eqs" to ensure compatibility with results from Kwan & Chan (2011).

Note: We recommend setting fixed.x = FALSE when generating standardized estimates and confidence intervals to model the variances and covariances of the exogenous observed variables if they are assumed to be random. If fixed.x = TRUE, which is the default setting in lavaan, MC() will fix the variances and the covariances of the exogenous observed variables to the sample values.

fit <- sem(
  model = model, mimic = "eqs", fixed.x = FALSE,
  sample.cov = list(covs_hongkong, covs_japan, covs_korea),
  sample.nobs = list(nobs_hongkong, nobs_japan, nobs_korea)
)

Standardized Monte Carlo Confidence Intervals

Standardized Monte Carlo Confidence intervals can be generated by passing the result of the MC() function to the MCStd() function.

unstd <- MC(fit, R = 20000L, alpha = 0.05)
MCStd(unstd, alpha = 0.05)
#> Standardized Monte Carlo Confidence Intervals
#>                est     se     R    2.5%   97.5%
#> gamma1.g1   0.0568 0.0191 20000  0.0194  0.0941
#> gamma2.g1   0.1985 0.0186 20000  0.1615  0.2355
#> gamma3.g1   0.2500 0.0150 20000  0.2208  0.2789
#> Y1~~Y1      0.8215 0.0103 20000  0.8006  0.8410
#> X1~~X1      1.0000 0.0000 20000  1.0000  1.0000
#> X1~~X2      0.6917 0.0077 20000  0.6764  0.7064
#> X1~~X3      0.4702 0.0115 20000  0.4476  0.4922
#> X2~~X2      1.0000 0.0000 20000  1.0000  1.0000
#> X2~~X3      0.4471 0.0118 20000  0.4238  0.4700
#> X3~~X3      1.0000 0.0000 20000  1.0000  1.0000
#> gamma1.g2   0.1390 0.0164 20000  0.1068  0.1712
#> gamma2.g2   0.1792 0.0158 20000  0.1479  0.2099
#> gamma3.g2   0.1688 0.0139 20000  0.1416  0.1961
#> Y1~~Y1.g2   0.8371 0.0088 20000  0.8196  0.8539
#> X1~~X1.g2   1.0000 0.0000 20000  1.0000  1.0000
#> X1~~X2.g2   0.6525 0.0075 20000  0.6375  0.6669
#> X1~~X3.g2   0.5023 0.0097 20000  0.4831  0.5209
#> X2~~X2.g2   1.0000 0.0000 20000  1.0000  1.0000
#> X2~~X3.g2   0.4452 0.0103 20000  0.4247  0.4652
#> X3~~X3.g2   1.0000 0.0000 20000  1.0000  1.0000
#> gamma1.g3   0.0863 0.0170 20000  0.0527  0.1193
#> gamma2.g3   0.2557 0.0164 20000  0.2234  0.2877
#> gamma3.g3   0.2289 0.0139 20000  0.2016  0.2565
#> Y1~~Y1.g3   0.7761 0.0103 20000  0.7556  0.7959
#> X1~~X1.g3   1.0000 0.0000 20000  1.0000  1.0000
#> X1~~X2.g3   0.6580 0.0079 20000  0.6425  0.6734
#> X1~~X3.g3   0.4738 0.0108 20000  0.4527  0.4947
#> X2~~X2.g3   1.0000 0.0000 20000  1.0000  1.0000
#> X2~~X3.g3   0.4353 0.0113 20000  0.4131  0.4571
#> X3~~X3.g3   1.0000 0.0000 20000  1.0000  1.0000
#> gamma1.g12 -0.0821 0.0251 20000 -0.1311 -0.0336
#> gamma1.g13 -0.0294 0.0257 20000 -0.0801  0.0208
#> gamma1.g23  0.0527 0.0236 20000  0.0070  0.0992
#> gamma2.g12  0.0193 0.0244 20000 -0.0288  0.0675
#> gamma2.g13 -0.0572 0.0248 20000 -0.1057 -0.0080
#> gamma2.g23 -0.0765 0.0228 20000 -0.1215 -0.0319
#> gamma3.g12  0.0811 0.0204 20000  0.0411  0.1208
#> gamma3.g13  0.0211 0.0204 20000 -0.0187  0.0613
#> gamma3.g23 -0.0601 0.0196 20000 -0.0987 -0.0217

References

Kwan, J. L. Y., & Chan, W. (2011). Comparing standardized coefficients in structural equation modeling: A model reparameterization approach. Behavior Research Methods, 43(3), 730–745. https://doi.org/10.3758/s13428-011-0088-6
Kwan, J. L. Y., & Chan, W. (2014). Comparing squared multiple correlation coefficients using structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 21(2), 225–238. https://doi.org/10.1080/10705511.2014.882673
Pesigan, I. J. A., & Cheung, S. F. (2023). Monte Carlo confidence intervals for the indirect effect with missing data. Behavior Research Methods. https://doi.org/10.3758/s13428-023-02114-4