Skip to contents

Example 5: Composite Reliability

Ivan Jacob Agaloos Pesigan

2024-04-14

Source: vignettes/example-5-composite-reliability.Rmd
example-5-composite-reliability.Rmd

In this example, the Monte Carlo method is used to generate confidence intervals for composite reliability using the Holzinger and Swineford (1939) data set.

data(HolzingerSwineford1939, package = "lavaan")

The confirmatory factor analysis model for \(X_{1}, \dots, X_{9}\) is given by

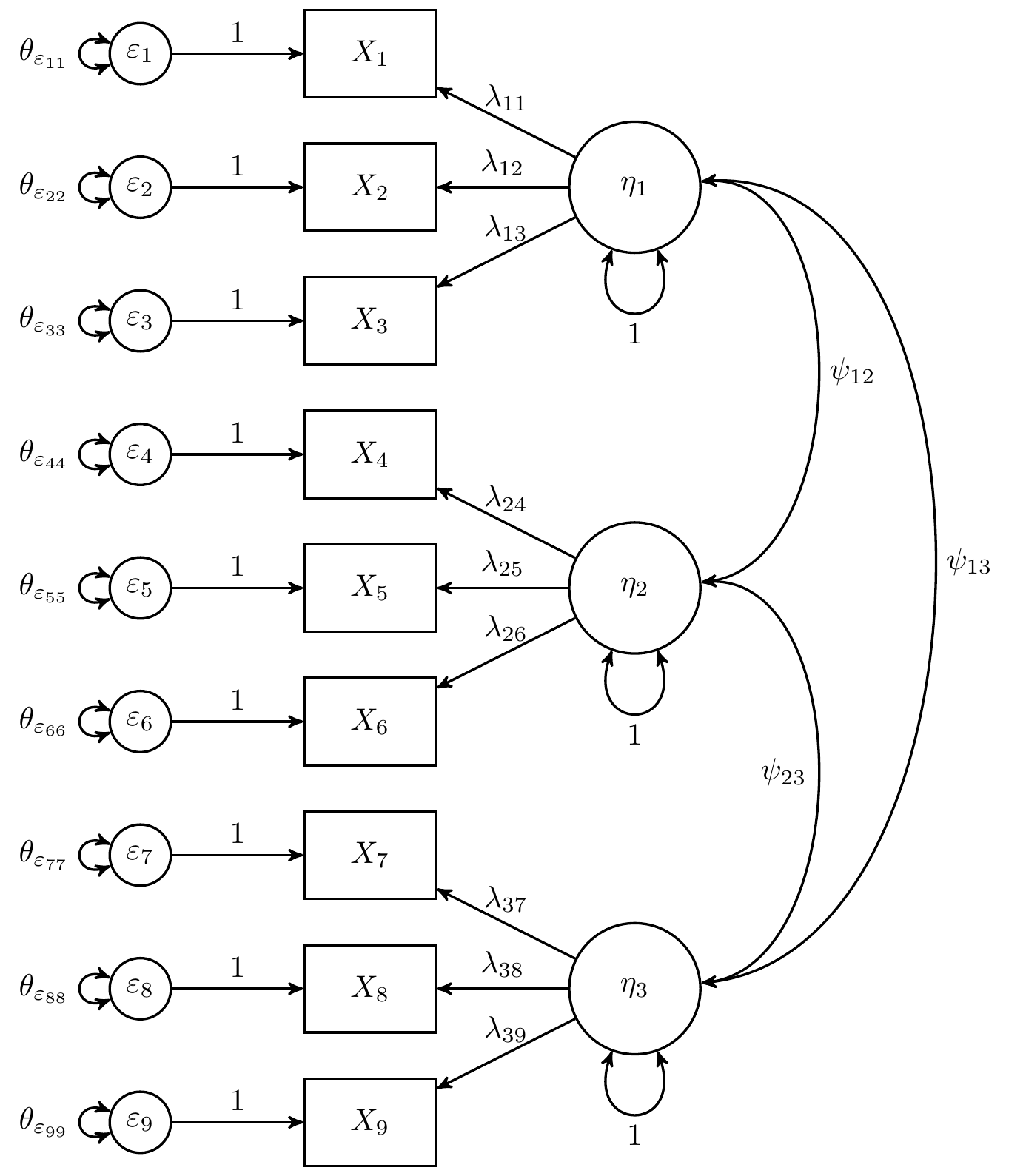
Three-Factor Confirmatory Factor Analysis Model
Three-Factor Confirmatory Factor Analysis Model

\(\eta_{1}\), \(\eta_{2}\), and \(\eta_{3}\) are the latent factors. \(\eta_{1}\) has three indicators \(X_{1}\), \(X_{2}\), and \(X_{3}\); \(\eta_{2}\) has three indicators \(X_{4}\), \(X_{5}\), and \(X_{6}\); and \(\eta_{3}\) has three indicators \(X_{7}\), \(X_{8}\), and \(X_{9}\) . The variances of \(\eta_{1}\), \(\eta_{2}\), and \(\eta_{3}\) are constrained to one.

Model Specification

Assuming that the latent variable variance is constrained to one, the omega total reliability coefficient is given by

\[ \omega_{\mathrm{total}} = \frac{ \left( \sum_{i = 1}^{k} \lambda_{i} \right)^2 }{ \left( \sum_{i = 1}^{k} \lambda_{i} \right)^2 + \sum_{i = 1}^{k} \theta_{\varepsilon_{ii}} } \]

where \(\lambda_{i}\) is the factor loading for item \(i\), \(\theta_{\varepsilon_{ii}}\) is the residual variance for item \(i\), and \(k\) is the number of items for a particular latent variable.

In the model specification below, the variances of the latent variables eta1, eta2, and eta3 are constrained to one, all the relevant parameters are labeled particularly the factor loadings and the error variances, and the omega total reliability coefficient per latent variable are defined using the := operator.

model <- "
  # fix latent variable variances to 1
  eta1 ~~ 1 * eta1
  eta2 ~~ 1 * eta2
  eta3 ~~ 1 * eta3
  # factor loadings
  eta1 =~ NA * x1 + l11 * x1 + l12 * x2 + l13 * x3
  eta2 =~ NA * x4 + l24 * x4 + l25 * x5 + l26 * x6
  eta3 =~ NA * x7 + l37 * x7 + l38 * x8 + l39 * x9
  # error variances
  x1 ~~ t1 * x1
  x2 ~~ t2 * x2
  x3 ~~ t3 * x3
  x4 ~~ t4 * x4
  x5 ~~ t5 * x5
  x6 ~~ t6 * x6
  x7 ~~ t7 * x7
  x8 ~~ t8 * x8
  x9 ~~ t9 * x9
  # composite reliability
  omega1 := (l11 + l12 + l13)^2 / ((l11 + l12 + l13)^2 + (t1 + t2 + t3))
  omega2 := (l24 + l25 + l26)^2 / ((l24 + l25 + l26)^2 + (t4 + t5 + t6))
  omega3 := (l37 + l38 + l39)^2 / ((l37 + l38 + l39)^2 + (t7 + t8 + t9))
"

Model Fitting

We can now fit the model using the cfa() function from lavaan.

fit <- cfa(model = model, data = HolzingerSwineford1939)

Monte Carlo Confidence Intervals

The fit lavaan object can then be passed to the MC() function to generate Monte Carlo confidence intervals.

MC(fit, R = 20000L, alpha = 0.05)
#> Monte Carlo Confidence Intervals
#>               est     se     R   2.5%  97.5%
#> eta1~~eta1 1.0000 0.0000 20000 1.0000 1.0000
#> eta2~~eta2 1.0000 0.0000 20000 1.0000 1.0000
#> eta3~~eta3 1.0000 0.0000 20000 1.0000 1.0000
#> l11        0.8996 0.0812 20000 0.7387 1.0576
#> l12        0.4979 0.0780 20000 0.3466 0.6547
#> l13        0.6562 0.0746 20000 0.5085 0.8021
#> l24        0.9897 0.0564 20000 0.8793 1.0995
#> l25        1.1016 0.0629 20000 0.9784 1.2239
#> l26        0.9166 0.0538 20000 0.8109 1.0207
#> l37        0.6195 0.0693 20000 0.4834 0.7549
#> l38        0.7309 0.0663 20000 0.5999 0.8598
#> l39        0.6700 0.0644 20000 0.5447 0.7972
#> t1         0.5491 0.1137 20000 0.3250 0.7731
#> t2         1.1338 0.1024 20000 0.9333 1.3311
#> t3         0.8443 0.0913 20000 0.6654 1.0256
#> t4         0.3712 0.0478 20000 0.2768 0.4646
#> t5         0.4463 0.0584 20000 0.3316 0.5612
#> t6         0.3562 0.0428 20000 0.2724 0.4396
#> t7         0.7994 0.0816 20000 0.6413 0.9564
#> t8         0.4877 0.0740 20000 0.3436 0.6330
#> t9         0.5661 0.0707 20000 0.4271 0.7054
#> eta1~~eta2 0.4585 0.0642 20000 0.3338 0.5867
#> eta1~~eta3 0.4705 0.0728 20000 0.3268 0.6125
#> eta2~~eta3 0.2830 0.0691 20000 0.1477 0.4194
#> omega1     0.6253 0.0366 20000 0.5489 0.6916
#> omega2     0.8852 0.0116 20000 0.8601 0.9057
#> omega3     0.6878 0.0313 20000 0.6216 0.7433

References

Pesigan, I. J. A., & Cheung, S. F. (2023). Monte Carlo confidence intervals for the indirect effect with missing data. Behavior Research Methods. https://doi.org/10.3758/s13428-023-02114-4