Benchmark: Comparing the Monte Carlo Method with Nonparametric Bootstrapping (MI)
Ivan Jacob Agaloos Pesigan
2025-10-19
Source:vignettes/benchmark-mi.Rmd
benchmark-mi.RmdWe compare the Monte Carlo (MC) method with nonparametric bootstrapping (NB) using the simple mediation model with missing data using multiple imputation. One advantage of MC over NB is speed. This is because the model is only fitted once in MC whereas it is fitted many times in NB.
Data
n <- 1000
a <- 0.50
b <- 0.50
cp <- 0.25
s2_em <- 1 - a^2
s2_ey <- 1 - cp^2 - a^2 * b^2 - b^2 * s2_em - 2 * cp * a * b
em <- rnorm(n = n, mean = 0, sd = sqrt(s2_em))
ey <- rnorm(n = n, mean = 0, sd = sqrt(s2_ey))
X <- rnorm(n = n)
M <- a * X + em
Y <- cp * X + b * M + ey
df <- data.frame(X, M, Y)
# Create data set with missing values.
miss <- sample(1:dim(df)[1], 300)
df[miss[1:100], "X"] <- NA
df[miss[101:200], "M"] <- NA
df[miss[201:300], "Y"] <- NAMultiple Imputation
Perform the appropriate multiple imputation approach to deal with missing values. In this example, we impute multivariate missing data under the normal model.
mi <- amelia(
x = df,
m = 5L,
p2s = 0
)Model Specification
The indirect effect is defined by the product of the slopes of paths
X to M labeled as a and
M to Y labeled as b. In this
example, we are interested in the confidence intervals of
indirect defined as the product of a and
b using the := operator in the
lavaan model syntax.
model <- "
Y ~ cp * X + b * M
M ~ a * X
X ~~ X
indirect := a * b
direct := cp
total := cp + (a * b)
"Model Fitting
We can now fit the model using the sem() function from
lavaan. We do not need to deal with missing values in this
stage.
fit <- sem(data = df, model = model)Monte Carlo Confidence Intervals (Multiple Imputation)
The fit lavaan object and mi
mids object can then be passed to the MCMI()
function from semmcci to generate Monte Carlo confidence
intervals using multiple imputation as described in Pesigan and Cheung
(2024).
MCMI(fit, R = 100L, alpha = 0.05, mi = mi)
#> Monte Carlo Confidence Intervals (Multiple Imputation Estimates)
#> est se R 2.5% 97.5%
#> cp 0.2274 0.0295 100 0.1787 0.2818
#> b 0.5192 0.0342 100 0.4534 0.5839
#> a 0.4790 0.0281 100 0.4249 0.5266
#> X~~X 1.0613 0.0443 100 0.9775 1.1328
#> Y~~Y 0.5439 0.0244 100 0.5010 0.5911
#> M~~M 0.7642 0.0397 100 0.7048 0.8397
#> indirect 0.2486 0.0189 100 0.2103 0.2755
#> direct 0.2274 0.0295 100 0.1787 0.2818
#> total 0.4760 0.0288 100 0.4243 0.5329Nonparametric Bootstrap Confidence Intervals (Multiple Imputation)
Nonparametric bootstrap confidence intervals can be generated in
bmemLavaan using the following.
summary(
bmemLavaan::bmem(data = df, model = model, method = "mi", boot = 100L, m = 5L)
)
#>
#> Estimate method: multiple imputation
#> Sample size: 1000
#> Number of request bootstrap draws: 100
#> Number of successful bootstrap draws: 100
#> Type of confidence interval: perc
#>
#> Values of statistics:
#>
#> Value SE 2.5% 97.5%
#> chisq 0.000 0.000 0.000 0.000
#> GFI 1.000 0.000 1.000 1.000
#> AGFI 1.000 0.000 1.000 1.000
#> RMSEA 0.000 0.000 0.000 0.000
#> NFI 1.000 0.000 1.000 1.000
#> NNFI 1.000 0.000 1.000 1.000
#> CFI 1.000 0.000 1.000 1.000
#> BIC 7742.967 81.777 7575.258 7857.675
#> SRMR 0.000 0.000 0.000 0.000
#>
#> Estimation of parameters:
#>
#> Estimate SE 2.5% 97.5%
#> Regressions:
#> Y ~
#> X (cp) 0.234 0.030 0.176 0.296
#> M (b) 0.513 0.032 0.460 0.570
#> M ~
#> X (a) 0.476 0.030 0.426 0.540
#>
#> Variances:
#> X 1.057 0.046 0.950 1.144
#> Y 0.556 0.027 0.488 0.600
#> M 0.755 0.035 0.684 0.813
#>
#>
#>
#> Defined parameters:
#> a*b (indr) 0.244 0.020 0.206 0.285
#> cp (drct) 0.234 0.030 0.176 0.296
#> cp+(*) (totl) 0.479 0.030 0.428 0.539Benchmark
benchmark_mi_01 <- microbenchmark(
MC = {
fit <- sem(
data = df,
model = model
)
mi <- Amelia::amelia(
x = df,
m = m,
p2s = 0
)
MCMI(
fit,
R = R,
decomposition = "chol",
pd = FALSE,
mi = mi
)
},
NB = bmemLavaan::bmem(
data = df,
model = model,
method = "mi",
boot = B,
m = m
),
times = 10
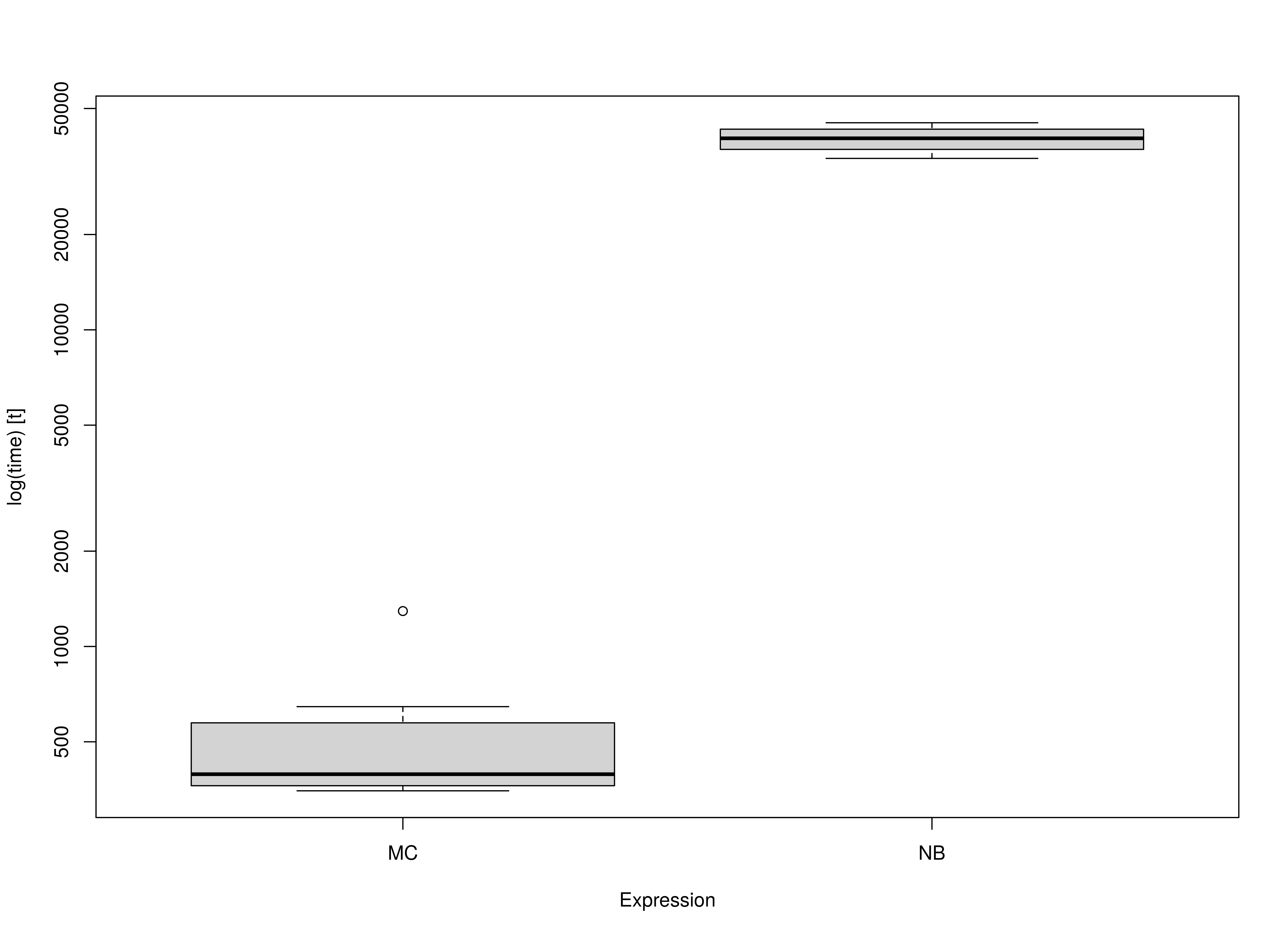
)Summary of Benchmark Results
summary(benchmark_mi_01, unit = "ms")
#> expr min lq mean median uq max neval
#> 1 MC 323.9427 330.8432 334.7035 332.8629 336.8628 354.5615 10
#> 2 NB 31060.0216 31177.9692 31271.3612 31229.8614 31333.7710 31534.5442 10Summary of Benchmark Results Relative to the Faster Method
summary(benchmark_mi_01, unit = "relative")
#> expr min lq mean median uq max neval
#> 1 MC 1.00000 1.00000 1.00000 1.000 1.00000 1.00000 10
#> 2 NB 95.88123 94.23791 93.43005 93.822 93.01642 88.93957 10Benchmark - Monte Carlo Method with Precalculated Estimates and Multiple Imputation
fit <- sem(
data = df,
model = model
)
mi <- Amelia::amelia(
x = df,
m = m,
p2s = 0
)
benchmark_mi_02 <- microbenchmark(
MC = MCMI(
fit,
R = R,
decomposition = "chol",
pd = FALSE,
mi = mi
),
NB = bmemLavaan::bmem(
data = df,
model = model,
method = "mi",
boot = B,
m = m
),
times = 10
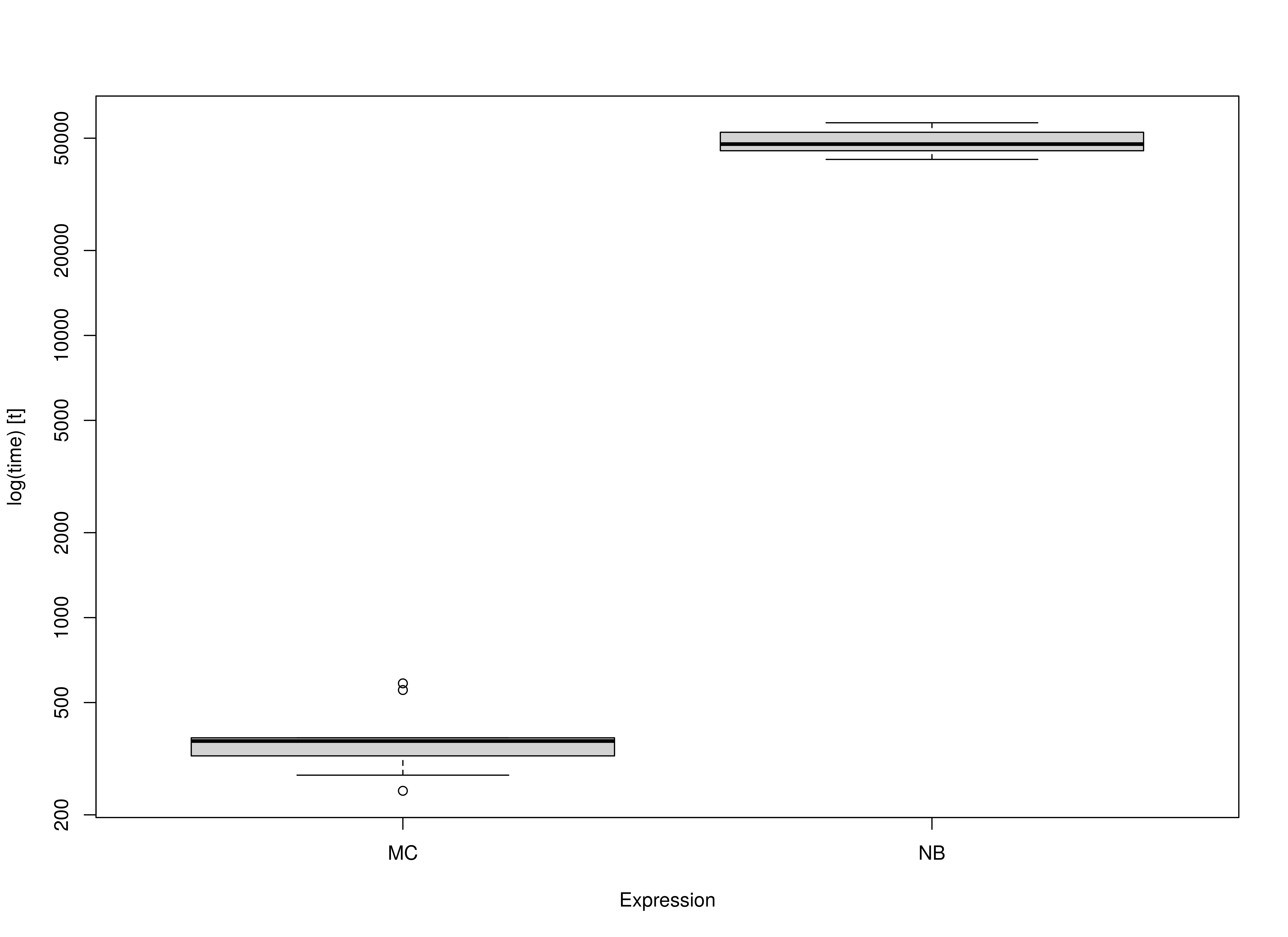
)Summary of Benchmark Results
summary(benchmark_mi_02, unit = "ms")
#> expr min lq mean median uq max neval
#> 1 MC 230.0875 235.618 257.2429 237.8043 244.8887 421.4892 10
#> 2 NB 30046.5756 30281.851 30532.2754 30478.7345 30647.8955 31290.6019 10Summary of Benchmark Results Relative to the Faster Method
summary(benchmark_mi_02, unit = "relative")
#> expr min lq mean median uq max neval
#> 1 MC 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 10
#> 2 NB 130.5876 128.5209 118.6905 128.1673 125.1503 74.2382 10