Skip to contents

Benchmark: Comparing the Monte Carlo Method with Nonparametric Bootstrapping

Ivan Jacob Agaloos Pesigan

2025-10-19

Source: vignettes/benchmark-complete.Rmd
benchmark-complete.Rmd

We compare the Monte Carlo (MC) method with nonparametric bootstrapping (NB) using the simple mediation model with complete data. One advantage of MC over NB is speed. This is because the model is only fitted once in MC whereas it is fitted many times in NB.

Data 

n <- 1000
a <- 0.50
b <- 0.50
cp <- 0.25
s2_em <- 1 - a^2
s2_ey <- 1 - cp^2 - a^2 * b^2 - b^2 * s2_em - 2 * cp * a * b
em <- rnorm(n = n, mean = 0, sd = sqrt(s2_em))
ey <- rnorm(n = n, mean = 0, sd = sqrt(s2_ey))
X <- rnorm(n = n)
M <- a * X + em
Y <- cp * X + b * M + ey
df <- data.frame(X, M, Y)

Model Specification

The indirect effect is defined by the product of the slopes of paths X to M labeled as a and M to Y labeled as b. In this example, we are interested in the confidence intervals of indirect defined as the product of a and b using the := operator in the lavaan model syntax.

model <- "
  Y ~ cp * X + b * M
  M ~ a * X
  X ~~ X
  indirect := a * b
  direct := cp
  total := cp + (a * b)
"

Model Fitting

We can now fit the model using the sem() function from lavaan.

fit <- sem(data = df, model = model)

Monte Carlo Confidence Intervals

The fit lavaan object can then be passed to the MC() function from semmcci to generate Monte Carlo confidence intervals.

MC(fit, R = 100L, alpha = 0.05)
#> Monte Carlo Confidence Intervals
#>             est     se   R   2.5%  97.5%
#> cp       0.2333 0.0296 100 0.1806 0.2903
#> b        0.5082 0.0279 100 0.4555 0.5527
#> a        0.4820 0.0280 100 0.4220 0.5301
#> X~~X     1.0590 0.0426 100 0.9751 1.1296
#> Y~~Y     0.5462 0.0231 100 0.5064 0.5959
#> M~~M     0.7527 0.0337 100 0.7024 0.8208
#> indirect 0.2449 0.0179 100 0.2058 0.2738
#> direct   0.2333 0.0296 100 0.1806 0.2903
#> total    0.4782 0.0295 100 0.4162 0.5283

Nonparametric Bootstrap Confidence Intervals

Nonparametric bootstrap confidence intervals can be generated in lavaan using the following.

parameterEstimates(
  sem(
    data = df,
    model = model,
    se = "bootstrap",
    bootstrap = 100L
  )
)
#>        lhs op      rhs    label   est    se      z pvalue ci.lower ci.upper
#> 1        Y  ~        X       cp 0.233 0.025  9.395      0    0.183    0.278
#> 2        Y  ~        M        b 0.508 0.028 18.057      0    0.454    0.568
#> 3        M  ~        X        a 0.482 0.026 18.550      0    0.433    0.535
#> 4        X ~~        X          1.059 0.046 23.224      0    0.969    1.161
#> 5        Y ~~        Y          0.546 0.023 23.640      0    0.508    0.593
#> 6        M ~~        M          0.753 0.033 23.131      0    0.692    0.814
#> 7 indirect :=      a*b indirect 0.245 0.020 12.443      0    0.209    0.289
#> 8   direct :=       cp   direct 0.233 0.025  9.395      0    0.183    0.278
#> 9    total := cp+(a*b)    total 0.478 0.027 17.966      0    0.418    0.518

Benchmark

Arguments

Variables Values Notes
R 1000 Number of Monte Carlo replications.
B 1000 Number of bootstrap samples. 
benchmark_complete_01 <- microbenchmark(
  MC = {
    fit <- sem(
      data = df,
      model = model
    )
    MC(
      fit,
      R = R,
      decomposition = "chol",
      pd = FALSE
    )
  },
  NB = sem(
    data = df,
    model = model,
    se = "bootstrap",
    bootstrap = B
  ),
  times = 10
)

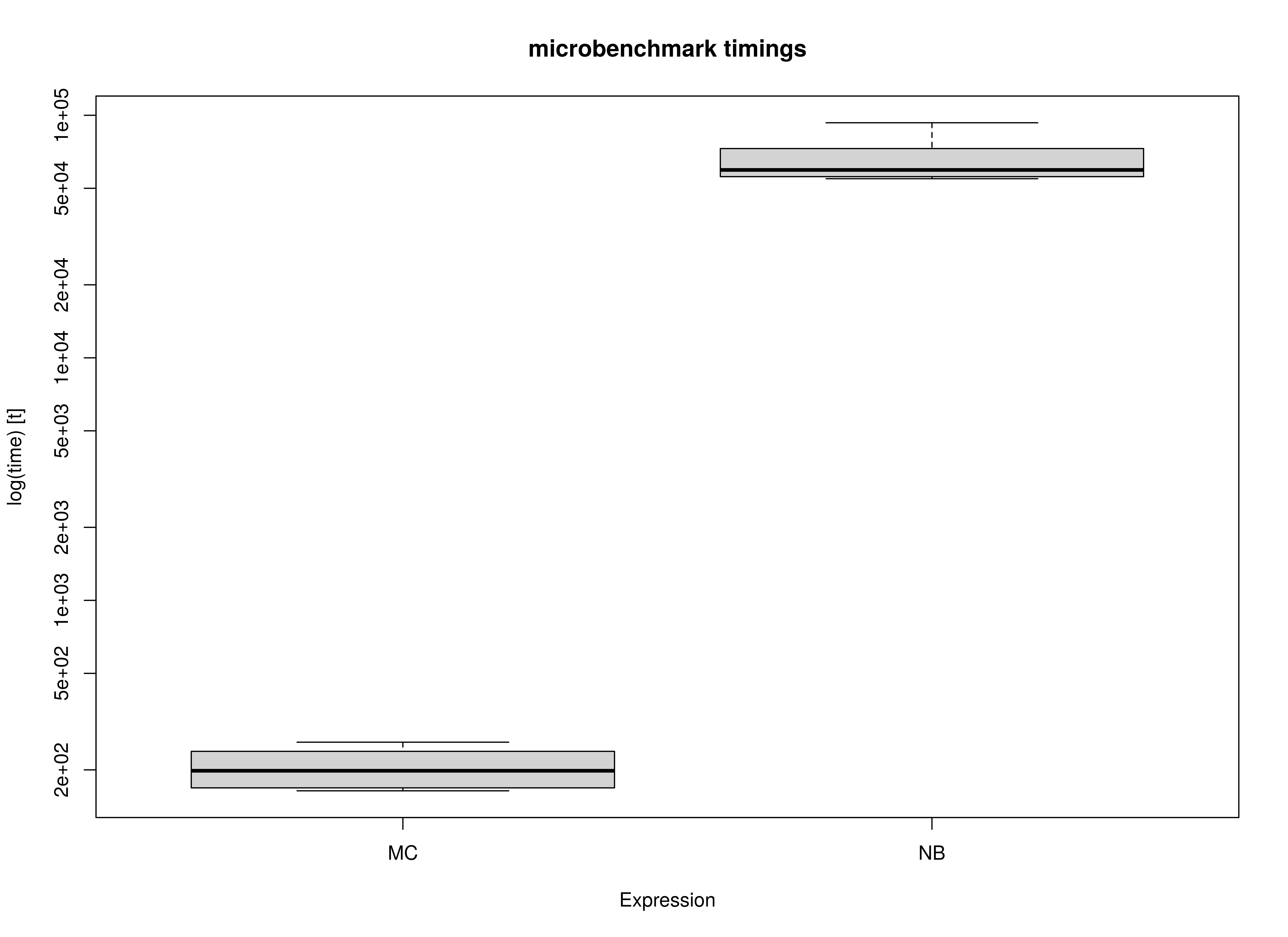
Summary of Benchmark Results 

summary(benchmark_complete_01, unit = "ms")
#>   expr         min          lq        mean      median          uq         max
#> 1   MC    71.92246    72.26498    75.40017    73.03176    74.11578    97.32907
#> 2   NB 13134.40864 13199.61712 13220.57029 13210.41936 13228.86796 13318.20412
#>   neval
#> 1    10
#> 2    10

Summary of Benchmark Results Relative to the Faster Method 

summary(benchmark_complete_01, unit = "relative")
#>   expr     min       lq     mean   median       uq      max neval
#> 1   MC   1.000   1.0000   1.0000   1.0000   1.0000   1.0000    10
#> 2   NB 182.619 182.6558 175.3387 180.8859 178.4892 136.8369    10

Plot

Benchmark - Monte Carlo Method with Precalculated Estimates 

fit <- sem(
  data = df,
  model = model
)
benchmark_complete_02 <- microbenchmark(
  MC = MC(
    fit,
    R = R,
    decomposition = "chol",
    pd = FALSE
  ),
  NB = sem(
    data = df,
    model = model,
    se = "bootstrap",
    bootstrap = B
  ),
  times = 10
)

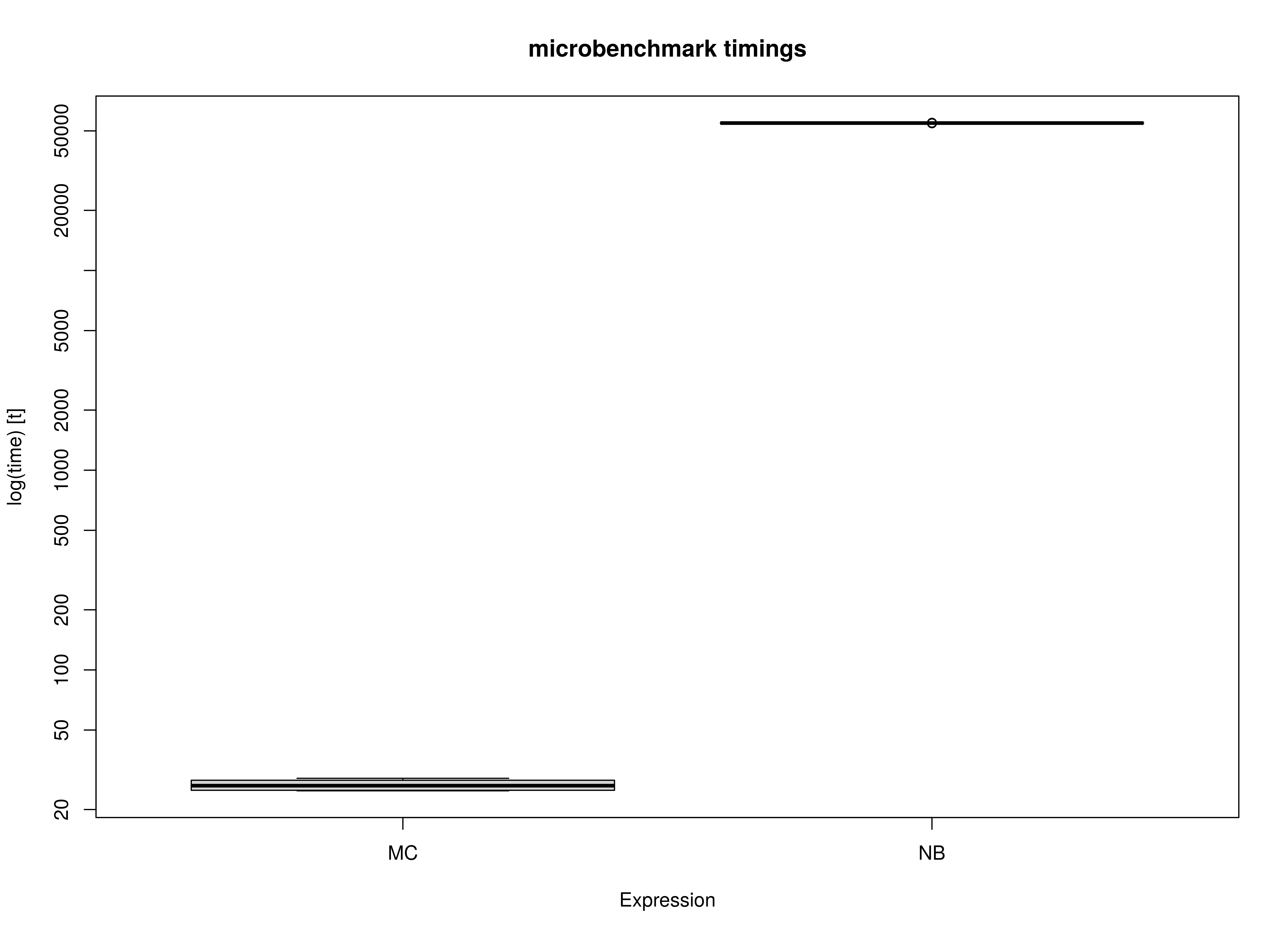
Summary of Benchmark Results 

summary(benchmark_complete_02, unit = "ms")
#>   expr         min          lq        mean      median         uq         max
#> 1   MC    21.42988    21.53643    22.90902    21.91124    25.2187    26.11223
#> 2   NB 13142.92047 13147.53284 13162.94078 13153.17865 13171.4634 13204.09618
#>   neval
#> 1    10
#> 2    10

Summary of Benchmark Results Relative to the Faster Method 

summary(benchmark_complete_02, unit = "relative")
#>   expr     min       lq     mean   median       uq      max neval
#> 1   MC   1.000   1.0000   1.0000   1.0000   1.0000   1.0000    10
#> 2   NB 613.299 610.4787 574.5745 600.2937 522.2896 505.6671    10

Plot

References

Pesigan, I. J. A., & Cheung, S. F. (2024). Monte Carlo confidence intervals for the indirect effect with missing data. Behavior Research Methods, 56(3), 1678–1696. https://doi.org/10.3758/s13428-023-02114-4