Fit the Discrete-Time Vector Autoregressive Model By ID (Stable Reciprocal Regulation | 1000 Measurement Occasions)

Ivan Jacob Agaloos Pesigan

2025-10-23

Dynamics Description

The Stable Reciprocal Regulation process represents a bivariate dynamic system in which two latent psychological constructs—such as positive and negative affect—mutually influence each other over time. Each construct shows moderate self-regulation (autoregressive effects) and mild opposing cross-effects, reflecting an equilibrium-seeking mechanism characteristic of emotional balance.

Individuals vary in their self-regulatory tendencies and in the strength of these antagonistic couplings. At the population level, the transition matrix indicates that increases in one construct are followed by slight decreases in the other, producing a stable, damped oscillatory pattern around individual equilibrium points. The process noise covariance allows for small correlated disturbances, while measurement errors are assumed to be minimal and symmetric across indicators.

This dynamic pattern captures a psychologically plausible process of reciprocal inhibition—where short-term fluctuations in one system component (e.g., positive affect) are naturally counteracted by adjustments in its counterpart (e.g., negative affect), leading to emotional homeostasis over time.

Model

The measurement model is given by $$\begin{equation} \mathbf{y}_{i, t} = \boldsymbol{\nu}_{i} + \boldsymbol{\Lambda} \boldsymbol{\eta}_{i, t} + \boldsymbol{\varepsilon}_{i, t}, \quad \mathrm{with} \quad \boldsymbol{\varepsilon}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \boldsymbol{\Theta} \right) \end{equation}$$ where $\mathbf{y}_{i, t}$, $\boldsymbol{\eta}_{i, t}$, and $\boldsymbol{\varepsilon}_{i, t}$ are random variables and $\boldsymbol{\nu}_{i}$, $\boldsymbol{\Lambda}$, and $\boldsymbol{\Theta}$ are model parameters. $\mathbf{y}_{i, t}$ represents a vector of observed random variables, $\boldsymbol{\eta}_{i, t}$ a vector of latent random variables, and $\boldsymbol{\varepsilon}_{i, t}$ a vector of random measurement errors, at time $t$ and individual $i$. $\boldsymbol{\Lambda}$ denotes a matrix of factor loadings, and $\boldsymbol{\Theta}$ the covariance matrix of $\boldsymbol{\varepsilon}$ that is invariant across individuals. In this model, $\boldsymbol{\Lambda}$ is an identity matrix and $\boldsymbol{\Theta}$ is a symmetric matrix.

The dynamic structure is given by $$\begin{equation} \boldsymbol{\eta}_{i, t} = \boldsymbol{\beta}_{i} \boldsymbol{\eta}_{i, t - 1} + \boldsymbol{\zeta}_{i, t}, \quad \mathrm{with} \quad \boldsymbol{\zeta}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \boldsymbol{\Psi} \right) \end{equation}$$ where $\boldsymbol{\eta}_{i, t}$, $\boldsymbol{\eta}_{i, t - 1}$, and $\boldsymbol{\zeta}_{i, t}$ are random variables, and $\boldsymbol{\beta}_{i}$, and $\boldsymbol{\Psi}$ are model parameters. Here, $\boldsymbol{\eta}_{i, t}$ is a vector of latent variables at time $t$ and individual $i$, $\boldsymbol{\eta}_{i, t - 1}$ represents a vector of latent variables at time $t - 1$ and individual $i$, and $\boldsymbol{\zeta}_{i, t}$ represents a vector of dynamic noise at time $t$ and individual $i$. $\boldsymbol{\beta}_{i}$ is a matrix of autoregression and cross regression coefficients for individual $i$, and $\boldsymbol{\Psi}$ the covariance matrix of $\boldsymbol{\zeta}_{i, t}$ that is invariant across all individuals. In this model, $\boldsymbol{\Psi}$ is a symmetric matrix.

Data Generation

Notation

Let $t = 1000$ be the number of time points and $n = 100$ be the number of individuals. We simulate a total of time $= 11000$ points per individual, discarding the first $10000$ as burn-in. The analysis uses the final $1000$ measurement occasions.

Let the measurement model intercept vector $\boldsymbol{\nu}$ be normally distributed with the following means

$$\begin{equation} \left( \begin{array}{c} 0.5 \\ -0.5 \\ \end{array} \right) \end{equation}$$

and covariance matrix

$$\begin{equation} \left( \begin{array}{cc} 0.1 & -0.05 \\ -0.05 & 0.1 \\ \end{array} \right) . \end{equation}$$

Let the factor loadings matrix $\boldsymbol{\Lambda}$ be given by

$$\begin{equation} \boldsymbol{\Lambda} = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right) . \end{equation}$$

Let the measurement error covariance matrix $\boldsymbol{\Theta}$ be given by

$$\begin{equation} \boldsymbol{\Theta} = \left( \begin{array}{cc} 0.5 & 0 \\ 0 & 0.5 \\ \end{array} \right) . \end{equation}$$

Let the initial condition $\boldsymbol{\eta}_{0}$ be given by

$$\begin{equation} \boldsymbol{\eta}_{0} \sim \mathcal{N} \left( \boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}, \boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0} \right) . \end{equation}$$

$\boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}$ and $\boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0}$ are functions of $\boldsymbol{\alpha}$ and $\boldsymbol{\beta}$.

Let the transition matrix $\boldsymbol{\beta}$ be normally distributed with the following means

$$\begin{equation} \left( \begin{array}{cc} 0.7 & -0.2 \\ -0.15 & 0.65 \\ \end{array} \right) \end{equation}$$

and covariance matrix

$$\begin{equation} \left( \begin{array}{cccc} 0.02 & 0.01 & 0 & 0 \\ 0.01 & 0.015 & 0 & 0 \\ 0 & 0 & 0.01 & 0.005 \\ 0 & 0 & 0.005 & 0.015 \\ \end{array} \right) . \end{equation}$$

Let the intercept vector $\boldsymbol{\alpha}$ be fixed to a zero vector.

The SimNuN and SimBetaN functions from the simStateSpace package generate random intercept vectors and transition matrices from the multivariate normal distribution. Note that the SimBetaN function generates transition matrices that are weakly stationary with an option to set lower and upper bounds.

Let the dynamic process noise $\boldsymbol{\Psi}$ be given by

$$\begin{equation} \boldsymbol{\Psi} = \left( \begin{array}{cc} 0.2 & -0.05 \\ -0.05 & 0.18 \\ \end{array} \right) . \end{equation}$$

R Function Arguments

n
#> [1] 100
time
#> [1] 11000
burnin
#> [1] 10000
# first mu0 in the list of length n
mu0[[1]]
#> [1] 0 0
# first sigma0 in the list of length n
sigma0[[1]]
#>            [,1]       [,2]
#> [1,]  0.3230830 -0.1220195
#> [2,] -0.1220195  0.5527409
# first sigma0_l in the list of length n
sigma0_l[[1]] # sigma0_l <- t(chol(sigma0))
#>            [,1]      [,2]
#> [1,]  0.5684039 0.0000000
#> [2,] -0.2146704 0.7117988
alpha
#> [[1]]
#> [1] 0 0
# first beta in the list of length n
beta[[1]]
#>            [,1]       [,2]
#> [1,]  0.6248343 0.02174497
#> [2,] -0.1054576 0.79427204
# first psi in the list of length n
psi[[1]]
#>       [,1]  [,2]
#> [1,]  0.20 -0.05
#> [2,] -0.05  0.18
psi_l[[1]] # psi_l <- t(chol(psi))
#>            [,1]      [,2]
#> [1,]  0.4472136 0.0000000
#> [2,] -0.1118034 0.4092676
# first nu in the list of length n
nu[[1]]
#> [1]  0.4832070 -0.7620639
lambda
#> [[1]]
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1
# first theta in the list of length n
theta[[1]]
#>      [,1] [,2]
#> [1,]  0.5  0.0
#> [2,]  0.0  0.5
theta_l[[1]] # theta_l <- t(chol(theta))
#>           [,1]      [,2]
#> [1,] 0.7071068 0.0000000
#> [2,] 0.0000000 0.7071068

Visualizing the Dynamics Without Process Noise and Measurement Error (n = 5 with Different Initial Condition)

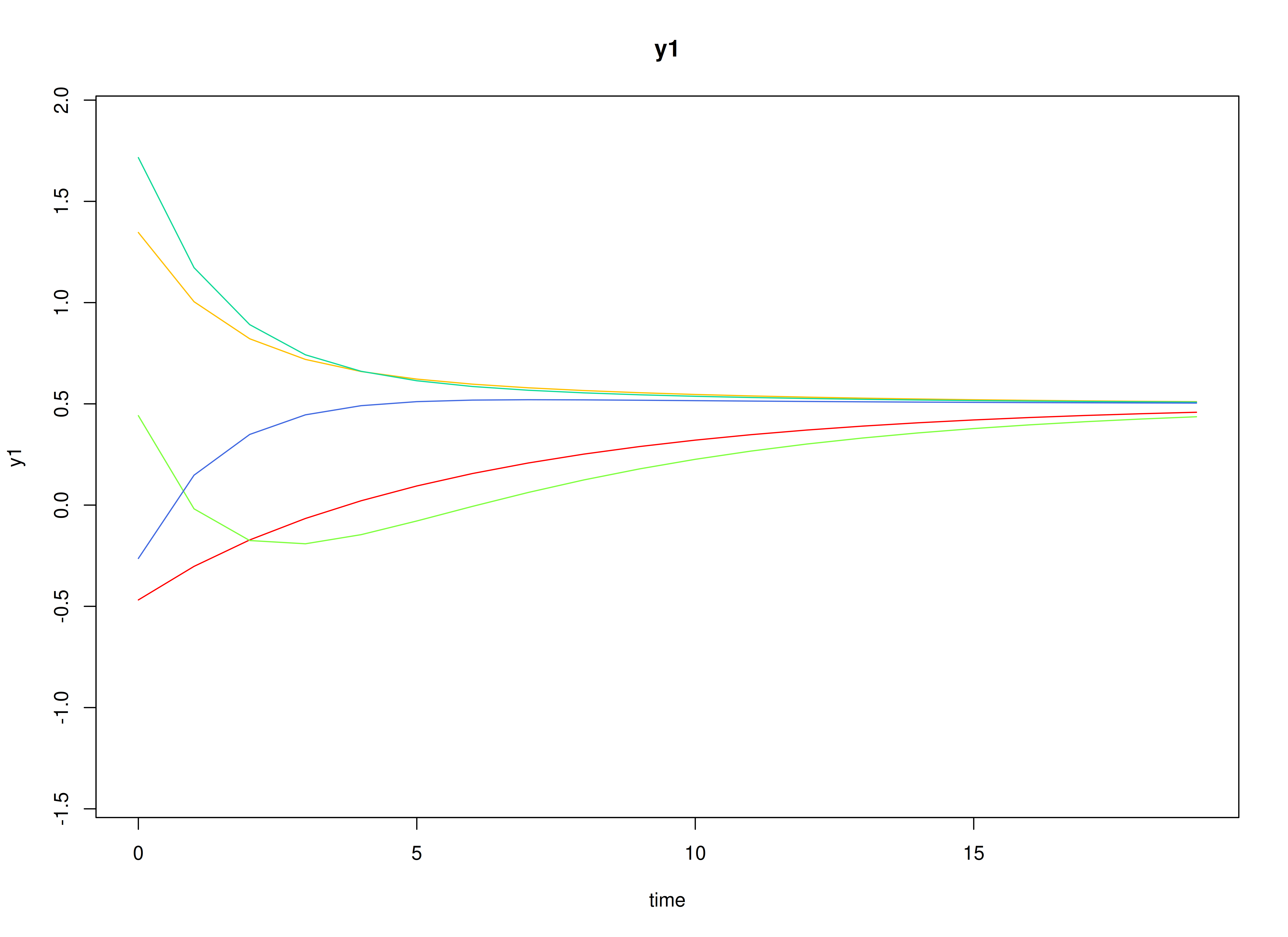
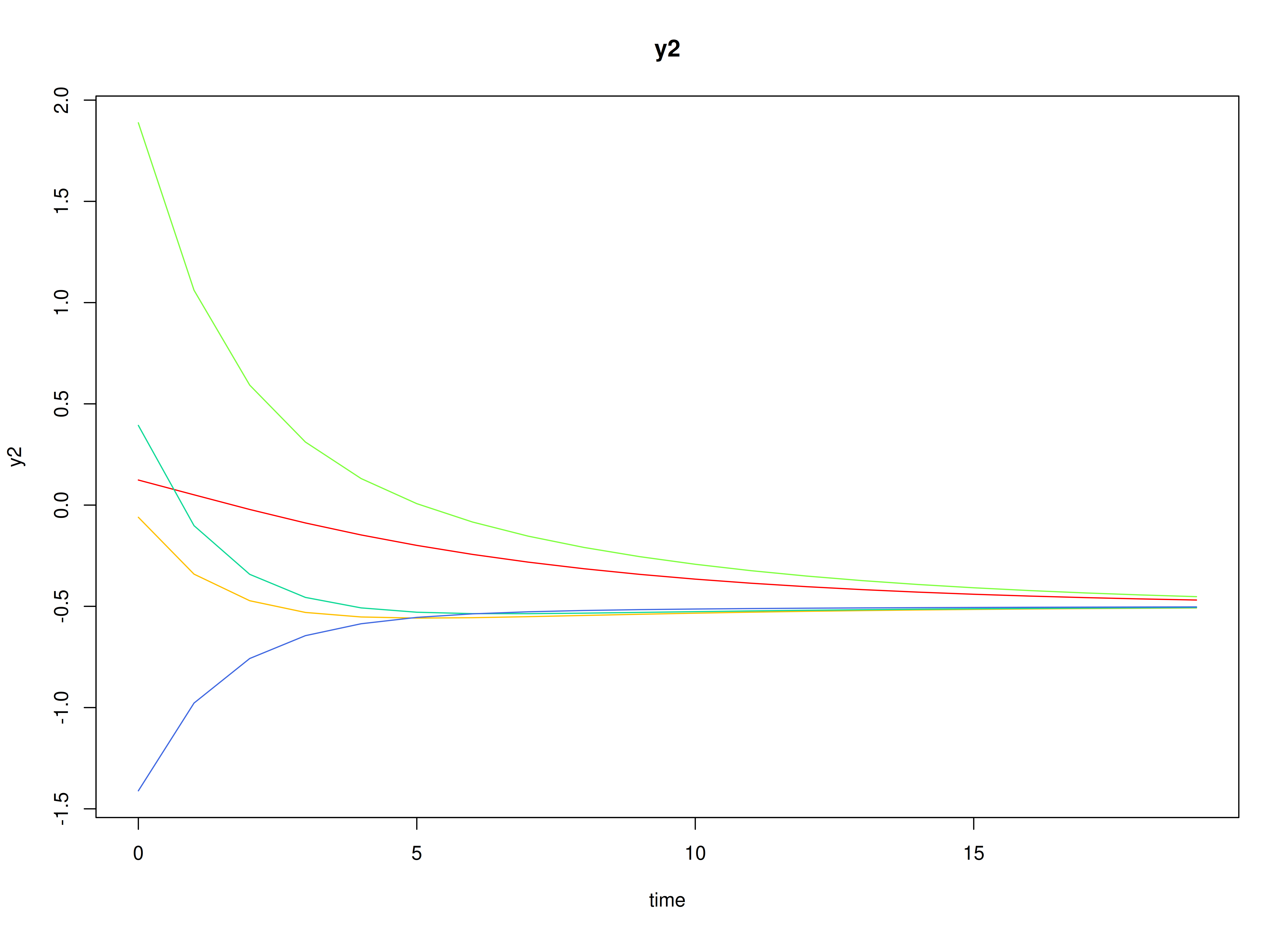
Using the SimSSMIVary Function from the simStateSpace Package to Simulate Data

library(simStateSpace)
sim <- SimSSMIVary(
  n = n,
  time = time,
  mu0 = mu0,
  sigma0_l = sigma0_l,
  alpha = alpha,
  beta = beta,
  psi_l = psi_l,
  nu = nu,
  lambda = lambda,
  theta_l = theta_l
)
data <- as.data.frame(sim, burnin = burnin)
head(data)
#>   id time         y1         y2
#> 1  1    0  0.2789887 -0.8588146
#> 2  1    1  1.7403454 -2.6296446
#> 3  1    2  1.6616097 -2.8627551
#> 4  1    3  1.5364391 -2.8515134
#> 5  1    4  1.3548295 -3.3594792
#> 6  1    5 -1.4337840 -1.2245788
plot(sim, burnin = burnin)

Model Fitting

library(OpenMx)
library(fitDTVARMxID)

The FitDTVARMxID function fits a DT-VAR model on each individual $i$. To set up the estimation, we first provide starting values for each parameter matrix.

Autoregressive Parameters (beta)

We initialize the autoregressive coefficient matrix $\boldsymbol{\beta}$ with the true values used in simulation.

beta_values <- beta

Intercepts (nu)

The intercept vector $\boldsymbol{\nu}$ is initialized with starting values.

nu_values <- nu

LDL’-parameterized covariance matrices

Covariances such as psi and theta are estimated using the LDL’ decomposition of a positive definite covariance matrix. The decomposition expresses a covariance matrix $\Sigma$ as

$$\begin{equation} \boldsymbol{\Sigma} = \left( \mathbf{L} + \mathbf{I} \right) \mathrm{diag} \left( \mathrm{Softplus} \left( \mathbf{d}_{uc} \right) \right) \left( \mathbf{L} + \mathbf{I} \right)^{\prime}, \end{equation}$$

where:

• $\mathbf{L}$ is a strictly lower-triangular matrix of free parameters (l_mat_strict),
  
• $\mathbf{I}$ is the identity matrix,
  
• $\mathbf{d}_{uc}$ is an unconstrained vector,
  
• $\mathrm{Softplus} \left(\mathbf{d}_{uc} \right) = \log \left(1 + \exp \left( \mathbf{d}_{uc} \right) \right)$ ensures strictly positive diagonal entries.

The LDL() function extracts this decomposition from a positive definite covariance matrix. It returns:

• d_uc: unconstrained diagonal parameters, equal to InvSoftplus(d_vec),
  
• d_vec: diagonal entries, equal to Softplus(d_uc),
  
• l_mat_strict: the strictly lower-triangular factor.

sigma <- matrix(
  data = c(1.0, 0.5, 0.5, 1.0),
  nrow = 2,
  ncol = 2
)

ldl_sigma <- LDL(sigma)
d_uc <- ldl_sigma$d_uc
l_mat_strict <- ldl_sigma$l_mat_strict
I <- diag(2)
sigma_reconstructed <- (l_mat_strict + I) %*% diag(log1p(exp(d_uc)), 2) %*% t(l_mat_strict + I)
sigma_reconstructed
#>      [,1] [,2]
#> [1,]  1.0  0.5
#> [2,]  0.5  1.0

Process Noise Covariance Matrix (psi)

Starting values for the process noise covariance matrix $\boldsymbol{\Psi}$ are given below, with corresponding LDL’ parameters.

psi_values <- psi[[1]]
ldl_psi_values <- LDL(psi_values)
psi_d_values <- ldl_psi_values$d_uc
psi_l_values <- ldl_psi_values$l_mat_strict

psi_d_values
#> [1] -1.507772 -1.701853

psi_l_values
#>       [,1] [,2]
#> [1,]  0.00    0
#> [2,] -0.25    0

Measurement Error Covariance Matrix (theta)

Starting values for the measurement error covariance matrix $\boldsymbol{\Theta}$ are given below, with corresponding LDL’ parameters.

theta_values <- theta[[1]]
ldl_theta_values <- LDL(theta_values)
theta_d_values <- ldl_theta_values$d_uc
theta_l_values <- ldl_theta_values$l_mat_strict

theta_d_values
#> [1] -0.4327521 -0.4327521

theta_l_values
#>      [,1] [,2]
#> [1,]    0    0
#> [2,]    0    0

Initial mean vector (mu_0) and covariance matrix (sigma_0)

The initial mean vector $\boldsymbol{\mu_0}$ and covariance matrix $\boldsymbol{\Sigma_0}$ are fixed using mu0 and sigma0.

mu0_values <- mu0

sigma0_values <- lapply(
  X = sigma0,
  FUN = LDL
)
sigma0_d_values <- lapply(
  X = sigma0_values,
  FUN = function(i) {
    i$d_uc
  }
)
sigma0_l_values <- lapply(
  X = sigma0_values,
  FUN = function(i) {
    i$l_mat_strict
  }
)

FitDTVARMxID

fit <- FitDTVARMxID(
  data = data,
  observed = c("y1", "y2"),
  id = "id",
  beta_values = beta_values,
  psi_d_values = psi_d_values,
  psi_l_values = psi_l_values,
  nu_values = nu_values,
  theta_d_values = theta_d_values,
  mu0_values = mu0_values,
  sigma0_d_values = sigma0_d_values,
  sigma0_l_values = sigma0_l_values,
  ncores = parallel::detectCores()
)

Parameter estimates

summary(fit, converged = FALSE)
#> Call:
#> FitDTVARMxID(data = data, observed = c("y1", "y2"), id = "id", 
#>     beta_values = beta_values, psi_d_values = psi_d_values, psi_l_values = psi_l_values, 
#>     nu_values = nu_values, theta_d_values = theta_d_values, mu0_values = mu0_values, 
#>     sigma0_d_values = sigma0_d_values, sigma0_l_values = sigma0_l_values, 
#>     ncores = parallel::detectCores())
#> 
#> Estimated paramaters per individual.
#>                              beta_1_1 beta_2_1 beta_1_2 beta_2_2  nu_1_1
#> FitDTVARMxID_DTVAR_ID1.Rds     0.5368  -0.0702  -0.0707   0.7654  0.4365
#> FitDTVARMxID_DTVAR_ID2.Rds     0.6047  -0.1689  -0.2031   0.8713  0.4224
#> FitDTVARMxID_DTVAR_ID3.Rds     0.5598  -0.1132  -0.3040   0.5022  0.8829
#> FitDTVARMxID_DTVAR_ID4.Rds     0.4775  -0.2401  -0.3301   0.7128  1.0040
#> FitDTVARMxID_DTVAR_ID5.Rds     0.7414   0.0059  -0.0867   0.8470  0.2039
#> FitDTVARMxID_DTVAR_ID6.Rds     0.5894  -0.0330  -0.0460   0.7211  0.7293
#> FitDTVARMxID_DTVAR_ID7.Rds     0.9505  -1.6717   0.0135   0.1441  0.7696
#> FitDTVARMxID_DTVAR_ID8.Rds     0.7771  -0.0045  -0.2708   0.8247  0.2779
#> FitDTVARMxID_DTVAR_ID9.Rds     0.8972   0.0036  -0.1295   0.4869  0.8428
#> FitDTVARMxID_DTVAR_ID10.Rds    0.7094  -0.0411  -0.0564   0.4701  0.5650
#> FitDTVARMxID_DTVAR_ID11.Rds    0.8959  -0.3061   0.0368   0.6398 -0.0812
#> FitDTVARMxID_DTVAR_ID12.Rds    0.7939  -0.3391  -0.0520   0.1682  0.6930
#> FitDTVARMxID_DTVAR_ID13.Rds    0.6511  -0.2074  -0.0293   0.7394  0.0939
#> FitDTVARMxID_DTVAR_ID14.Rds    0.6553  -0.0507  -0.3202   0.8014  0.8675
#> FitDTVARMxID_DTVAR_ID15.Rds    0.7177  -0.0361  -0.4268   0.7310  0.8138
#> FitDTVARMxID_DTVAR_ID16.Rds    0.9042   0.0176  -0.1156   0.5051  0.6429
#> FitDTVARMxID_DTVAR_ID17.Rds    0.3023  -0.4424  -0.1555   0.7332  0.9775
#> FitDTVARMxID_DTVAR_ID18.Rds    0.6927  -0.3386  -0.1735   0.6288  0.0577
#> FitDTVARMxID_DTVAR_ID19.Rds    0.8009   0.0069  -0.2469   0.5225  0.3198
#> FitDTVARMxID_DTVAR_ID20.Rds    0.9232   0.1540  -0.0964   0.6475  0.6039
#> FitDTVARMxID_DTVAR_ID21.Rds    0.3881  -0.0431  -0.2227   0.8225  1.0008
#> FitDTVARMxID_DTVAR_ID22.Rds    0.6551  -0.0711  -0.1119   0.7459  0.8224
#> FitDTVARMxID_DTVAR_ID23.Rds    0.8886  -0.0175  -0.1945   0.6767  0.4544
#> FitDTVARMxID_DTVAR_ID24.Rds    0.7282   0.0503  -0.3111   0.8068  0.2221
#> FitDTVARMxID_DTVAR_ID25.Rds    0.9194  -0.1655   0.0319   0.6714  0.6033
#> FitDTVARMxID_DTVAR_ID26.Rds    0.8239   0.0280  -0.2835   0.8514  0.6963
#> FitDTVARMxID_DTVAR_ID27.Rds    0.7268  -0.0989  -0.2623   0.5200  0.4145
#> FitDTVARMxID_DTVAR_ID28.Rds    0.3337  -0.1490  -0.8768   0.6792  0.2765
#> FitDTVARMxID_DTVAR_ID29.Rds    0.7182  -0.2828   0.0155   0.5219  0.6221
#> FitDTVARMxID_DTVAR_ID30.Rds    0.0238  -0.1170  -0.3774   0.6713  0.2464
#> FitDTVARMxID_DTVAR_ID31.Rds    0.8878  -0.0340  -0.1248   0.7845  0.6925
#> FitDTVARMxID_DTVAR_ID32.Rds    0.4795  -0.3669  -0.1546   0.7720  0.6023
#> FitDTVARMxID_DTVAR_ID33.Rds    0.5033  -0.3288  -0.2408   0.5599  0.7319
#> FitDTVARMxID_DTVAR_ID34.Rds    0.5268  -0.2858  -0.1943   0.7663  0.4871
#> FitDTVARMxID_DTVAR_ID35.Rds    0.8412  -0.0330  -0.0709   0.7810  0.3291
#> FitDTVARMxID_DTVAR_ID36.Rds    0.5567  -0.2399  -0.0589   0.6456  0.3149
#> FitDTVARMxID_DTVAR_ID37.Rds    0.1992  -0.1493  -0.5465   0.8314  0.7875
#> FitDTVARMxID_DTVAR_ID38.Rds    0.4735  -0.2233  -0.4155   0.7706  0.2817
#> FitDTVARMxID_DTVAR_ID39.Rds    0.6843  -0.1289  -0.1254   0.4991  0.6100
#> FitDTVARMxID_DTVAR_ID40.Rds    0.8702  -0.3220   0.1448   0.3503  0.4375
#> FitDTVARMxID_DTVAR_ID41.Rds    0.7403  -0.2958   0.1181   0.6637  0.4080
#> FitDTVARMxID_DTVAR_ID42.Rds    0.7135  -0.0402  -0.1453   0.8884  0.2259
#> FitDTVARMxID_DTVAR_ID43.Rds    0.5692   0.0023  -0.4641   0.9493  0.5738
#> FitDTVARMxID_DTVAR_ID44.Rds    0.7086  -0.1449  -0.2021   0.6659  0.1718
#> FitDTVARMxID_DTVAR_ID45.Rds    0.6405  -0.2231  -0.2573   0.6735  0.4977
#> FitDTVARMxID_DTVAR_ID46.Rds    0.1279  -0.0309  -1.2086   0.7669  0.7253
#> FitDTVARMxID_DTVAR_ID47.Rds    0.8665  -0.2528  -0.1514   0.1041  0.5503
#> FitDTVARMxID_DTVAR_ID48.Rds    0.2590  -0.1600  -0.4111   0.7358  0.6339
#> FitDTVARMxID_DTVAR_ID49.Rds    0.6096  -0.2047  -0.2474   0.6606  0.3095
#> FitDTVARMxID_DTVAR_ID50.Rds    0.8035  -0.1507  -0.0550   0.6995  0.8673
#> FitDTVARMxID_DTVAR_ID51.Rds    0.4670  -0.2864  -0.2441   0.6133  0.6809
#> FitDTVARMxID_DTVAR_ID53.Rds    0.6250  -0.1793  -0.2858   0.4800  0.7430
#> FitDTVARMxID_DTVAR_ID54.Rds    0.1342  -0.0588  -0.5755   0.7795 -0.0384
#> FitDTVARMxID_DTVAR_ID55.Rds    0.1200   0.0175  -1.1847   0.7136  0.7774
#> FitDTVARMxID_DTVAR_ID56.Rds    0.7204  -0.2406  -0.0450   0.7555  0.5184
#> FitDTVARMxID_DTVAR_ID57.Rds    0.6350  -0.0708  -0.1610   0.8001  0.7129
#> FitDTVARMxID_DTVAR_ID58.Rds    0.2791  -0.1851   0.0440   0.6796  0.5854
#> FitDTVARMxID_DTVAR_ID59.Rds    0.8151  -0.3587  -0.0207   0.6042  0.4989
#> FitDTVARMxID_DTVAR_ID60.Rds    0.7484  -0.1546  -0.0867   0.7712 -0.3376
#> FitDTVARMxID_DTVAR_ID61.Rds    0.9611   0.0868  -0.2103   0.7315  0.7430
#> FitDTVARMxID_DTVAR_ID62.Rds    0.7355  -0.4368  -0.1413   0.5764  0.2569
#> FitDTVARMxID_DTVAR_ID63.Rds    0.8133  -0.1563  -0.1488   0.6623  0.4454
#> FitDTVARMxID_DTVAR_ID64.Rds    0.7784  -0.0147  -0.1267   0.7339  0.5774
#> FitDTVARMxID_DTVAR_ID65.Rds    0.8324  -0.2593  -0.0035   0.6866 -0.0013
#> FitDTVARMxID_DTVAR_ID66.Rds    0.4536  -0.1836  -0.5256   0.7116  0.3174
#> FitDTVARMxID_DTVAR_ID67.Rds    0.6178  -0.1982  -0.2362   0.7421  0.4661
#> FitDTVARMxID_DTVAR_ID68.Rds    0.8143  -0.2173  -0.1673   0.6744  0.4489
#> FitDTVARMxID_DTVAR_ID69.Rds    0.1627  -0.0623  -0.9035   0.8181  0.8693
#> FitDTVARMxID_DTVAR_ID70.Rds    0.1614  -0.0308  -0.9435   0.7473  0.7474
#> FitDTVARMxID_DTVAR_ID71.Rds    0.8216  -0.4116  -0.0083   0.1156  0.3077
#> FitDTVARMxID_DTVAR_ID72.Rds    0.2373  -0.1118  -0.3332   0.7850  0.7144
#> FitDTVARMxID_DTVAR_ID73.Rds    0.7291  -0.1645  -0.1513   0.2115  0.5826
#> FitDTVARMxID_DTVAR_ID74.Rds    0.5982  -0.2361  -0.2008   0.5023  0.5349
#> FitDTVARMxID_DTVAR_ID75.Rds    0.1977  -0.1403  -0.1057   0.8879  0.6917
#> FitDTVARMxID_DTVAR_ID76.Rds    0.6761  -0.3994  -0.2860   0.4336  0.7090
#> FitDTVARMxID_DTVAR_ID77.Rds    0.5907  -0.1167  -0.3919   0.6799  0.1841
#> FitDTVARMxID_DTVAR_ID78.Rds    0.8584  -0.1863  -0.1015   0.4941  0.1772
#> FitDTVARMxID_DTVAR_ID79.Rds    0.7719  -0.2933  -0.0781   0.5043  0.9801
#> FitDTVARMxID_DTVAR_ID80.Rds    0.7156  -0.2341  -0.1202   0.6356  0.2607
#> FitDTVARMxID_DTVAR_ID81.Rds    0.7448  -0.1541  -0.1447   0.8418  0.2891
#> FitDTVARMxID_DTVAR_ID82.Rds    0.6264  -0.2270  -0.2846   0.6703  1.0152
#> FitDTVARMxID_DTVAR_ID83.Rds    0.3904  -0.1280  -0.6043   0.5848  0.4930
#> FitDTVARMxID_DTVAR_ID84.Rds    0.4162  -0.1891  -0.0991   0.8660  0.1803
#> FitDTVARMxID_DTVAR_ID85.Rds    0.7183  -0.4555  -0.0719   0.5080  0.6134
#> FitDTVARMxID_DTVAR_ID86.Rds    0.8250   0.0250  -0.7644   0.9016  0.6633
#> FitDTVARMxID_DTVAR_ID87.Rds    0.6970  -0.1445  -0.0875   0.4955  0.5399
#> FitDTVARMxID_DTVAR_ID88.Rds    0.7496  -0.2242  -0.3302   0.4261  0.7416
#> FitDTVARMxID_DTVAR_ID89.Rds    0.7432  -0.1672  -0.1312   0.6684  0.5417
#> FitDTVARMxID_DTVAR_ID90.Rds    0.7909  -0.1420  -0.1057   0.5595  0.6422
#> FitDTVARMxID_DTVAR_ID91.Rds    0.9099  -0.4773   0.1267   0.5580  0.1474
#> FitDTVARMxID_DTVAR_ID92.Rds    0.7082   0.0492  -0.0969   0.4881  0.0762
#> FitDTVARMxID_DTVAR_ID93.Rds    0.4507  -0.1125  -0.0060   0.9117  0.4992
#> FitDTVARMxID_DTVAR_ID94.Rds    0.4803  -0.1497  -0.1249   0.8451  0.0749
#> FitDTVARMxID_DTVAR_ID95.Rds    0.5847  -0.0250  -0.1401   0.7062  0.9707
#> FitDTVARMxID_DTVAR_ID96.Rds    0.8034  -0.4989  -0.0261   0.5808  0.8310
#> FitDTVARMxID_DTVAR_ID97.Rds    0.5907  -0.2541  -0.2149   0.4245  0.8430
#> FitDTVARMxID_DTVAR_ID98.Rds    0.5349  -0.4894  -0.0568   0.6810  0.7698
#> FitDTVARMxID_DTVAR_ID99.Rds    1.0165  -0.3363   0.1280   0.5734  0.1782
#> FitDTVARMxID_DTVAR_ID100.Rds   0.7594   0.0735  -0.2106   0.5557  0.1576
#>                               nu_2_1 psi_l_2_1 psi_d_1_1 psi_d_2_1 theta_d_1_1
#> FitDTVARMxID_DTVAR_ID1.Rds   -0.8186   -0.1078   -1.2678   -1.8718     -0.4864
#> FitDTVARMxID_DTVAR_ID2.Rds   -0.2992   -0.0599   -0.9256   -1.8233     -0.5986
#> FitDTVARMxID_DTVAR_ID3.Rds   -0.2875   -0.2167   -1.2697   -1.0067     -0.5444
#> FitDTVARMxID_DTVAR_ID4.Rds   -1.2026   -0.1997   -1.4222   -1.9234     -0.4614
#> FitDTVARMxID_DTVAR_ID5.Rds   -0.1513   -0.2348   -1.5016   -2.1197     -0.4957
#> FitDTVARMxID_DTVAR_ID6.Rds   -0.7579   -0.2557   -1.2945   -1.7400     -0.4874
#> FitDTVARMxID_DTVAR_ID7.Rds   -0.4398    0.2365   -3.2708   -0.5271     -0.0809
#> FitDTVARMxID_DTVAR_ID8.Rds   -0.2561   -0.2608   -1.5913   -2.5883     -0.3531
#> FitDTVARMxID_DTVAR_ID9.Rds   -1.0128   -0.3291   -1.3525   -1.0513     -0.4782
#> FitDTVARMxID_DTVAR_ID10.Rds  -0.3813   -0.5487   -2.0490   -1.3935     -0.2147
#> FitDTVARMxID_DTVAR_ID11.Rds   0.2441   -0.6474   -2.3654   -2.4103     -0.3092
#> FitDTVARMxID_DTVAR_ID12.Rds  -0.2974   -0.3960   -1.7132   -0.0971     -0.5663
#> FitDTVARMxID_DTVAR_ID13.Rds  -0.8756   -0.1691   -2.3676   -1.5070     -0.1467
#> FitDTVARMxID_DTVAR_ID14.Rds  -0.6405   -0.2048   -1.4373   -2.3551     -0.3424
#> FitDTVARMxID_DTVAR_ID15.Rds  -0.9309   -0.3741   -1.4395   -2.2871     -0.3011
#> FitDTVARMxID_DTVAR_ID16.Rds  -1.3052   -0.3038   -1.4028   -1.6035     -0.4150
#> FitDTVARMxID_DTVAR_ID17.Rds  -1.0469   -0.0691   -1.0696   -1.8057     -0.5895
#> FitDTVARMxID_DTVAR_ID18.Rds  -0.2183   -0.0320   -1.3791   -1.2958     -0.4440
#> FitDTVARMxID_DTVAR_ID19.Rds  -0.2151   -0.4034   -1.6073   -1.6257     -0.3908
#> FitDTVARMxID_DTVAR_ID20.Rds  -0.1232   -0.1033   -1.5053   -2.0244     -0.4460
#> FitDTVARMxID_DTVAR_ID21.Rds  -0.9387   -0.2698   -1.2289   -2.4130     -0.5344
#> FitDTVARMxID_DTVAR_ID22.Rds  -0.9231   -0.2668   -1.2739   -2.1707     -0.6564
#> FitDTVARMxID_DTVAR_ID23.Rds  -0.2167   -0.3842   -1.5091   -1.2985     -0.4699
#> FitDTVARMxID_DTVAR_ID24.Rds  -0.3065   -0.3596   -1.6906   -2.9461     -0.4053
#> FitDTVARMxID_DTVAR_ID25.Rds  -0.9135   -0.3815   -1.6550   -1.6728     -0.4503
#> FitDTVARMxID_DTVAR_ID26.Rds  -0.5230   -0.2145   -1.3142   -2.6137     -0.5673
#> FitDTVARMxID_DTVAR_ID27.Rds  -0.2679   -0.1841   -1.1600   -1.7503     -0.5093
#> FitDTVARMxID_DTVAR_ID28.Rds  -0.3739    0.0375   -0.5565   -2.4539     -1.2898
#> FitDTVARMxID_DTVAR_ID29.Rds  -0.6901   -0.2014   -1.4639   -1.0015     -0.3869
#> FitDTVARMxID_DTVAR_ID30.Rds  -0.1468   -0.0881   -0.1277   -1.5647    -16.7613
#> FitDTVARMxID_DTVAR_ID31.Rds  -0.7532   -0.2316   -1.6426   -1.8208     -0.4810
#> FitDTVARMxID_DTVAR_ID32.Rds  -0.7063   -0.3114   -1.3900   -2.1506     -0.4060
#> FitDTVARMxID_DTVAR_ID33.Rds  -0.7320   -0.2747   -1.2611   -1.1319     -0.5615
#> FitDTVARMxID_DTVAR_ID34.Rds  -0.4032   -0.1424   -1.1576   -1.6508     -0.7280
#> FitDTVARMxID_DTVAR_ID35.Rds  -0.4713   -0.3272   -1.3506   -2.0352     -0.3799
#> FitDTVARMxID_DTVAR_ID36.Rds  -0.3874   -0.4142   -1.4847   -1.6102     -0.4478
#> FitDTVARMxID_DTVAR_ID37.Rds  -0.4460   -0.0831    0.1669   -1.8004    -17.6548
#> FitDTVARMxID_DTVAR_ID38.Rds   0.1787   -0.1553   -0.9243   -2.1750     -0.8365
#> FitDTVARMxID_DTVAR_ID39.Rds  -0.5671   -0.1813   -1.7107   -1.5890     -0.4363
#> FitDTVARMxID_DTVAR_ID40.Rds  -0.6076   -0.5792   -1.9429   -2.1186     -0.3083
#> FitDTVARMxID_DTVAR_ID41.Rds  -0.8709   -0.4104   -2.0604   -1.6461     -0.2518
#> FitDTVARMxID_DTVAR_ID42.Rds  -0.3322   -0.4759   -1.5696   -2.4494     -0.3158
#> FitDTVARMxID_DTVAR_ID43.Rds  -0.6324   -0.3349   -1.4301   -2.9113     -0.4389
#> FitDTVARMxID_DTVAR_ID44.Rds   0.1245   -0.3152   -1.3288   -1.3969     -0.5877
#> FitDTVARMxID_DTVAR_ID45.Rds  -0.4897   -0.0740   -1.4421   -2.1886     -0.4042
#> FitDTVARMxID_DTVAR_ID46.Rds  -0.7909   -0.0132   -0.0291   -3.0097    -16.8888
#> FitDTVARMxID_DTVAR_ID47.Rds  -0.2790   -0.2880   -1.2610   -0.0094     -0.4721
#> FitDTVARMxID_DTVAR_ID48.Rds  -0.6186   -0.1168    0.1868   -1.8646    -17.5831
#> FitDTVARMxID_DTVAR_ID49.Rds  -0.0980   -0.3025   -1.5063   -1.5169     -0.3390
#> FitDTVARMxID_DTVAR_ID50.Rds  -0.8974   -0.3857   -1.7880   -1.9753     -0.4222
#> FitDTVARMxID_DTVAR_ID51.Rds  -0.2619   -0.1665   -1.0795   -1.5672     -0.5673
#> FitDTVARMxID_DTVAR_ID53.Rds  -0.4883   -0.2893   -1.4623   -1.4744     -0.4075
#> FitDTVARMxID_DTVAR_ID54.Rds  -0.0352   -0.1149    0.0472   -2.2328    -17.4471
#> FitDTVARMxID_DTVAR_ID55.Rds  -0.8772   -0.0372   -0.1191   -2.6756    -17.5457
#> FitDTVARMxID_DTVAR_ID56.Rds  -0.1177   -0.5471   -1.6436   -2.2556     -0.3799
#> FitDTVARMxID_DTVAR_ID57.Rds  -0.9229   -0.2858   -1.2825   -1.4648     -0.3813
#> FitDTVARMxID_DTVAR_ID58.Rds  -0.5437   -0.2561   -0.4939   -1.5080     -1.1625
#> FitDTVARMxID_DTVAR_ID59.Rds  -0.3164   -0.2588   -1.5142   -2.0303     -0.3351
#> FitDTVARMxID_DTVAR_ID60.Rds   0.0361   -0.2464   -2.0308   -1.7677     -0.3545
#> FitDTVARMxID_DTVAR_ID61.Rds  -0.3095   -0.0743   -1.4020   -1.6253     -0.4189
#> FitDTVARMxID_DTVAR_ID62.Rds  -0.8477   -0.5532   -2.0846   -2.5670     -0.2218
#> FitDTVARMxID_DTVAR_ID63.Rds  -0.3810   -0.2416   -1.5317   -1.7179     -0.3716
#> FitDTVARMxID_DTVAR_ID64.Rds  -1.0208   -0.2625   -1.8440   -1.8998     -0.3523
#> FitDTVARMxID_DTVAR_ID65.Rds  -0.2738   -0.1106   -1.6085   -1.3010     -0.5094
#> FitDTVARMxID_DTVAR_ID66.Rds   0.0291   -0.0243   -1.0289   -2.0305     -0.7830
#> FitDTVARMxID_DTVAR_ID67.Rds  -0.6303   -0.3232   -1.8052   -1.8289     -0.3780
#> FitDTVARMxID_DTVAR_ID68.Rds  -0.5011   -0.5114   -2.0702   -1.8586     -0.2291
#> FitDTVARMxID_DTVAR_ID69.Rds  -0.8128   -0.0817   -0.5316   -2.3532     -1.8511
#> FitDTVARMxID_DTVAR_ID70.Rds  -0.6871   -0.1054    0.1214   -2.7485    -14.4938
#> FitDTVARMxID_DTVAR_ID71.Rds  -0.3513   -0.4413   -1.5188   -0.0916     -0.4850
#> FitDTVARMxID_DTVAR_ID72.Rds  -0.0550   -0.0845    0.1787   -1.6041    -14.5908
#> FitDTVARMxID_DTVAR_ID73.Rds  -0.4599   -0.3696   -1.1877   -0.3475     -0.4350
#> FitDTVARMxID_DTVAR_ID74.Rds  -0.5147   -0.1825   -1.1510   -0.9712     -0.6207
#> FitDTVARMxID_DTVAR_ID75.Rds  -0.3207   -0.1519    0.1180   -1.2786    -16.0555
#> FitDTVARMxID_DTVAR_ID76.Rds  -0.7265   -0.0957   -1.3980   -1.2517     -0.5104
#> FitDTVARMxID_DTVAR_ID77.Rds  -0.3651   -0.0596   -1.4824   -1.7902     -0.4481
#> FitDTVARMxID_DTVAR_ID78.Rds  -0.5543   -0.4073   -1.7081   -1.5099     -0.3321
#> FitDTVARMxID_DTVAR_ID79.Rds  -0.6850   -0.1969   -1.5904   -1.1463     -0.3809
#> FitDTVARMxID_DTVAR_ID80.Rds  -0.2242   -0.3744   -1.4970   -1.9062     -0.4120
#> FitDTVARMxID_DTVAR_ID81.Rds  -0.1612   -0.3533   -1.5620   -2.0535     -0.4271
#> FitDTVARMxID_DTVAR_ID82.Rds  -0.6030   -0.1117   -1.2599   -1.8670     -0.6551
#> FitDTVARMxID_DTVAR_ID83.Rds  -0.3834   -0.0331   -0.6808   -2.1689     -1.0931
#> FitDTVARMxID_DTVAR_ID84.Rds  -0.2357   -0.0752   -1.3544   -1.8956     -0.4848
#> FitDTVARMxID_DTVAR_ID85.Rds  -0.8496   -0.1624   -1.4520   -1.5721     -0.4110
#> FitDTVARMxID_DTVAR_ID86.Rds  -0.4205   -0.0915   -1.8187   -4.0982     -0.4230
#> FitDTVARMxID_DTVAR_ID87.Rds  -0.7060   -0.4005   -1.3192   -1.8216     -0.4579
#> FitDTVARMxID_DTVAR_ID88.Rds  -0.2934   -0.3042   -1.3025   -1.6486     -0.5690
#> FitDTVARMxID_DTVAR_ID89.Rds  -0.3553   -0.2244   -1.1492   -1.7873     -0.5482
#> FitDTVARMxID_DTVAR_ID90.Rds  -0.0101   -0.1548   -1.5718   -1.2709     -0.4520
#> FitDTVARMxID_DTVAR_ID91.Rds  -0.1130   -0.7217   -2.4966   -2.8544     -0.2596
#> FitDTVARMxID_DTVAR_ID92.Rds  -0.4147   -0.3314   -1.4094   -1.5648     -0.3608
#> FitDTVARMxID_DTVAR_ID93.Rds  -0.2751   -0.2785   -1.3578   -1.9514     -0.4260
#> FitDTVARMxID_DTVAR_ID94.Rds  -0.1443   -0.1568   -1.0855   -1.5183     -0.7822
#> FitDTVARMxID_DTVAR_ID95.Rds  -0.8549   -0.2497   -1.2258   -1.3600     -0.5683
#> FitDTVARMxID_DTVAR_ID96.Rds  -0.2594   -0.0807   -1.9423   -2.2158     -0.2944
#> FitDTVARMxID_DTVAR_ID97.Rds  -0.5098   -0.3307   -1.2669   -0.7536     -0.4292
#> FitDTVARMxID_DTVAR_ID98.Rds  -0.6860   -0.0557   -1.6351   -1.8480     -0.4059
#> FitDTVARMxID_DTVAR_ID99.Rds  -0.6418   -0.6898   -2.5043   -3.0653     -0.3960
#> FitDTVARMxID_DTVAR_ID100.Rds -0.6619   -0.4304   -1.4603   -1.1345     -0.4672
#>                              theta_d_2_1
#> FitDTVARMxID_DTVAR_ID1.Rds       -0.3585
#> FitDTVARMxID_DTVAR_ID2.Rds       -0.3691
#> FitDTVARMxID_DTVAR_ID3.Rds       -0.6200
#> FitDTVARMxID_DTVAR_ID4.Rds       -0.1997
#> FitDTVARMxID_DTVAR_ID5.Rds       -0.2650
#> FitDTVARMxID_DTVAR_ID6.Rds       -0.4538
#> FitDTVARMxID_DTVAR_ID7.Rds       -1.9898
#> FitDTVARMxID_DTVAR_ID8.Rds       -0.3748
#> FitDTVARMxID_DTVAR_ID9.Rds       -0.8890
#> FitDTVARMxID_DTVAR_ID10.Rds      -0.7310
#> FitDTVARMxID_DTVAR_ID11.Rds      -0.2609
#> FitDTVARMxID_DTVAR_ID12.Rds      -2.6570
#> FitDTVARMxID_DTVAR_ID13.Rds      -0.5390
#> FitDTVARMxID_DTVAR_ID14.Rds      -0.0859
#> FitDTVARMxID_DTVAR_ID15.Rds      -0.2692
#> FitDTVARMxID_DTVAR_ID16.Rds      -0.6065
#> FitDTVARMxID_DTVAR_ID17.Rds      -0.3817
#> FitDTVARMxID_DTVAR_ID18.Rds      -0.6433
#> FitDTVARMxID_DTVAR_ID19.Rds      -0.5183
#> FitDTVARMxID_DTVAR_ID20.Rds      -0.4017
#> FitDTVARMxID_DTVAR_ID21.Rds      -0.2738
#> FitDTVARMxID_DTVAR_ID22.Rds      -0.2047
#> FitDTVARMxID_DTVAR_ID23.Rds      -0.4376
#> FitDTVARMxID_DTVAR_ID24.Rds      -0.2619
#> FitDTVARMxID_DTVAR_ID25.Rds      -0.4330
#> FitDTVARMxID_DTVAR_ID26.Rds      -0.2718
#> FitDTVARMxID_DTVAR_ID27.Rds      -0.3111
#> FitDTVARMxID_DTVAR_ID28.Rds      -0.0650
#> FitDTVARMxID_DTVAR_ID29.Rds      -0.7339
#> FitDTVARMxID_DTVAR_ID30.Rds      -0.5452
#> FitDTVARMxID_DTVAR_ID31.Rds      -0.3616
#> FitDTVARMxID_DTVAR_ID32.Rds      -0.2456
#> FitDTVARMxID_DTVAR_ID33.Rds      -0.6863
#> FitDTVARMxID_DTVAR_ID34.Rds      -0.4742
#> FitDTVARMxID_DTVAR_ID35.Rds      -0.4387
#> FitDTVARMxID_DTVAR_ID36.Rds      -0.5271
#> FitDTVARMxID_DTVAR_ID37.Rds      -0.3479
#> FitDTVARMxID_DTVAR_ID38.Rds      -0.2698
#> FitDTVARMxID_DTVAR_ID39.Rds      -0.4725
#> FitDTVARMxID_DTVAR_ID40.Rds      -0.4270
#> FitDTVARMxID_DTVAR_ID41.Rds      -0.4718
#> FitDTVARMxID_DTVAR_ID42.Rds      -0.3196
#> FitDTVARMxID_DTVAR_ID43.Rds      -0.2205
#> FitDTVARMxID_DTVAR_ID44.Rds      -0.5171
#> FitDTVARMxID_DTVAR_ID45.Rds      -0.3218
#> FitDTVARMxID_DTVAR_ID46.Rds      -0.3164
#> FitDTVARMxID_DTVAR_ID47.Rds     -16.1762
#> FitDTVARMxID_DTVAR_ID48.Rds      -0.3090
#> FitDTVARMxID_DTVAR_ID49.Rds      -0.4923
#> FitDTVARMxID_DTVAR_ID50.Rds      -0.4467
#> FitDTVARMxID_DTVAR_ID51.Rds      -0.3265
#> FitDTVARMxID_DTVAR_ID53.Rds      -0.4867
#> FitDTVARMxID_DTVAR_ID54.Rds      -0.1062
#> FitDTVARMxID_DTVAR_ID55.Rds      -0.1234
#> FitDTVARMxID_DTVAR_ID56.Rds      -0.2880
#> FitDTVARMxID_DTVAR_ID57.Rds      -0.4785
#> FitDTVARMxID_DTVAR_ID58.Rds      -0.4102
#> FitDTVARMxID_DTVAR_ID59.Rds      -0.5090
#> FitDTVARMxID_DTVAR_ID60.Rds      -0.3194
#> FitDTVARMxID_DTVAR_ID61.Rds      -0.3857
#> FitDTVARMxID_DTVAR_ID62.Rds      -0.2595
#> FitDTVARMxID_DTVAR_ID63.Rds      -0.4839
#> FitDTVARMxID_DTVAR_ID64.Rds      -0.3040
#> FitDTVARMxID_DTVAR_ID65.Rds      -0.7939
#> FitDTVARMxID_DTVAR_ID66.Rds      -0.2010
#> FitDTVARMxID_DTVAR_ID67.Rds      -0.4367
#> FitDTVARMxID_DTVAR_ID68.Rds      -0.3292
#> FitDTVARMxID_DTVAR_ID69.Rds      -0.1423
#> FitDTVARMxID_DTVAR_ID70.Rds      -0.2082
#> FitDTVARMxID_DTVAR_ID71.Rds     -16.8122
#> FitDTVARMxID_DTVAR_ID72.Rds      -0.4539
#> FitDTVARMxID_DTVAR_ID73.Rds      -1.8710
#> FitDTVARMxID_DTVAR_ID74.Rds      -0.9003
#> FitDTVARMxID_DTVAR_ID75.Rds      -0.4793
#> FitDTVARMxID_DTVAR_ID76.Rds      -0.6042
#> FitDTVARMxID_DTVAR_ID77.Rds      -0.4764
#> FitDTVARMxID_DTVAR_ID78.Rds      -0.5706
#> FitDTVARMxID_DTVAR_ID79.Rds      -0.6519
#> FitDTVARMxID_DTVAR_ID80.Rds      -0.4353
#> FitDTVARMxID_DTVAR_ID81.Rds      -0.4321
#> FitDTVARMxID_DTVAR_ID82.Rds      -0.3854
#> FitDTVARMxID_DTVAR_ID83.Rds      -0.0711
#> FitDTVARMxID_DTVAR_ID84.Rds      -0.4290
#> FitDTVARMxID_DTVAR_ID85.Rds      -0.5423
#> FitDTVARMxID_DTVAR_ID86.Rds      -0.0082
#> FitDTVARMxID_DTVAR_ID87.Rds      -0.3419
#> FitDTVARMxID_DTVAR_ID88.Rds      -0.3758
#> FitDTVARMxID_DTVAR_ID89.Rds      -0.3947
#> FitDTVARMxID_DTVAR_ID90.Rds      -0.5436
#> FitDTVARMxID_DTVAR_ID91.Rds      -0.3294
#> FitDTVARMxID_DTVAR_ID92.Rds      -0.4484
#> FitDTVARMxID_DTVAR_ID93.Rds      -0.2371
#> FitDTVARMxID_DTVAR_ID94.Rds      -0.4731
#> FitDTVARMxID_DTVAR_ID95.Rds      -0.6297
#> FitDTVARMxID_DTVAR_ID96.Rds      -0.3520
#> FitDTVARMxID_DTVAR_ID97.Rds      -1.1530
#> FitDTVARMxID_DTVAR_ID98.Rds      -0.4772
#> FitDTVARMxID_DTVAR_ID99.Rds      -0.2744
#> FitDTVARMxID_DTVAR_ID100.Rds     -0.6998

Proportion of converged cases

converged(
  fit,
  theta_tol = 0.01,
  prop = TRUE
)
#> [1] 0.88

Fixed-Effect Meta-Analysis of Measurement Error

When fitting DT-VAR models per person, separating process noise ($\boldsymbol{\Psi}$) from measurement error ($\boldsymbol{\Theta}$) can be unstable for some individuals. To stabilize inference, we first pool the person-level $\boldsymbol{\Theta}_{i}$ estimates from only the converged fits using a fixed-effect meta-analysis. This yields a high-precision estimate of the common measurement-error covariance that we will then hold fixed in a second pass of model fitting.

What the code does: - Selects individuals that converged and whose $\boldsymbol{\Theta}_i$ diagonals exceed a small threshold (theta_tol), filtering out near-zero or ill-conditioned solutions. - Extracts each person’s LDL’ diagonal parameters for $\boldsymbol{\Theta}_i$ and their sampling covariance matrices. - Computes the inverse-variance-weighted pooled estimate (fixed effect), returning it on the same LDL’ parameterization used by FitDTVARMxID().

library(metaVAR)
fixed_theta <- MetaVARMx(
  fit,
  random = FALSE, # TRUE by default
  effects = FALSE, # TRUE by default
  cov_meas = TRUE, # FALSE by default
  theta_tol = 0.01
)

You can read summary(fixed_theta) as providing the pooled (fixed) measurement-error scale that is common across persons. If individual instruments truly share the same reliability structure, fixing $\boldsymbol{\Theta}$ to this pooled value improves stability and often reduces bias in the dynamic parameters.

Note: Fixed-effect pooling assumes a common $\boldsymbol{\Theta}$ across individuals.

coef(fixed_theta)
#>  alpha_1_1  alpha_2_1 
#> -0.4008133 -0.3456229
summary(fixed_theta)
#> Call:
#> MetaVARMx(object = fit, random = FALSE, effects = FALSE, cov_meas = TRUE, 
#>     theta_tol = 0.01)
#>                est     se        z p    2.5%   97.5%
#> alpha[1,1] -0.4008 0.0140 -28.6995 0 -0.4282 -0.3734
#> alpha[2,1] -0.3456 0.0134 -25.7253 0 -0.3720 -0.3193

theta_d_values <- coef(fixed_theta)

Refit the model with fixed measurement error covariance matrix

We refit the individual models using the pooled $\boldsymbol{\Theta}$ as a fixed measurement-error covariance matrix.

fit <- FitDTVARMxID(
  data = data,
  observed = c("y1", "y2"),
  id = "id",
  beta_values = beta_values,
  psi_d_values = psi_d_values,
  psi_l_values = psi_l_values,
  nu_values = nu_values,
  theta_fixed = TRUE,
  theta_d_values = theta_d_values,
  mu0_values = mu0_values,
  sigma0_d_values = sigma0_d_values,
  sigma0_l_values = sigma0_l_values,
  ncores = parallel::detectCores()
)

With $\boldsymbol{\Theta}$ fixed, the re-estimation focuses on the dynamic structure ($\boldsymbol{\beta}$, $\boldsymbol{\Psi}$) and intercepts ($\boldsymbol{\nu}$). In practice, this often increases the proportion of converged fits and yields more stable cross-lag estimates.

Proportion of converged cases

converged(
  fit,
  prop = TRUE
)
#> [1] 1

Random-Effects Meta-Analysis of Person-Specific Dynamics and Means

Having stabilized $\boldsymbol{\Theta}$, we synthesize the person-specific estimates to recover population-level effects and their between-person variability. We use a random-effects model so the pooled mean reflects both within-person estimation uncertainty and between-person heterogeneity.

random <- MetaVARMx(
  fit,
  effects = TRUE,
  int_meas = TRUE
)

summary(random)
#> Call:
#> MetaVARMx(object = fit, effects = TRUE, int_meas = TRUE)
#>                  est     se        z      p    2.5%   97.5%
#> alpha[1,1]    0.7022 0.0131  53.7051 0.0000  0.6766  0.7278
#> alpha[2,1]   -0.1531 0.0142 -10.7960 0.0000 -0.1808 -0.1253
#> alpha[3,1]   -0.1573 0.0120 -13.0906 0.0000 -0.1808 -0.1337
#> alpha[4,1]    0.6886 0.0125  55.2346 0.0000  0.6642  0.7131
#> alpha[5,1]    0.5127 0.0287  17.8583 0.0000  0.4564  0.5689
#> alpha[6,1]   -0.4849 0.0316 -15.3601 0.0000 -0.5468 -0.4230
#> tau_sqr[1,1]  0.0117 0.0022   5.4141 0.0000  0.0075  0.0160
#> tau_sqr[2,1]  0.0085 0.0019   4.3808 0.0000  0.0047  0.0122
#> tau_sqr[3,1] -0.0008 0.0014  -0.5507 0.5819 -0.0035  0.0020
#> tau_sqr[4,1] -0.0011 0.0014  -0.8032 0.4219 -0.0038  0.0016
#> tau_sqr[5,1] -0.0045 0.0038  -1.1836 0.2366 -0.0119  0.0029
#> tau_sqr[6,1]  0.0018 0.0039   0.4548 0.6493 -0.0059  0.0095
#> tau_sqr[2,2]  0.0148 0.0027   5.3881 0.0000  0.0094  0.0202
#> tau_sqr[3,2] -0.0021 0.0015  -1.3703 0.1706 -0.0051  0.0009
#> tau_sqr[4,2]  0.0003 0.0016   0.1647 0.8692 -0.0029  0.0034
#> tau_sqr[5,2] -0.0035 0.0040  -0.8603 0.3896 -0.0114  0.0044
#> tau_sqr[6,2] -0.0019 0.0043  -0.4361 0.6628 -0.0104  0.0066
#> tau_sqr[3,3]  0.0081 0.0019   4.3211 0.0000  0.0044  0.0117
#> tau_sqr[4,3]  0.0041 0.0014   2.8686 0.0041  0.0013  0.0070
#> tau_sqr[5,3] -0.0040 0.0032  -1.2613 0.2072 -0.0103  0.0022
#> tau_sqr[6,3] -0.0024 0.0035  -0.6964 0.4862 -0.0093  0.0044
#> tau_sqr[4,4]  0.0091 0.0020   4.4806 0.0000  0.0051  0.0131
#> tau_sqr[5,4] -0.0045 0.0034  -1.3298 0.1836 -0.0111  0.0021
#> tau_sqr[6,4] -0.0001 0.0037  -0.0181 0.9856 -0.0074  0.0073
#> tau_sqr[5,5]  0.0724 0.0112   6.4581 0.0000  0.0504  0.0944
#> tau_sqr[6,5] -0.0451 0.0103  -4.3825 0.0000 -0.0653 -0.0249
#> tau_sqr[6,6]  0.0907 0.0139   6.5363 0.0000  0.0635  0.1179
#> i_sqr[1,1]    0.9023 0.0163  55.4284 0.0000  0.8704  0.9342
#> i_sqr[2,1]    0.9328 0.0115  80.7789 0.0000  0.9101  0.9554
#> i_sqr[3,1]    0.9560 0.0070 136.5643 0.0000  0.9423  0.9697
#> i_sqr[4,1]    0.9628 0.0060 161.5206 0.0000  0.9512  0.9745
#> i_sqr[5,1]    0.9560 0.0065 146.7066 0.0000  0.9432  0.9687
#> i_sqr[6,1]    0.9746 0.0037 261.3841 0.0000  0.9673  0.9819

• The fixed part of the random-effects model gives pooled means $\boldsymbol{\alpha} = \mathbb{E} \left[ \mathrm{Vec} \left( \boldsymbol{\beta} \right), \boldsymbol{\nu} \right]$.
• The random part yields between-person covariances ($\boldsymbol{\tau}^{2}$) quantifying heterogeneity in dynamics ($\boldsymbol{\beta}$) and means ($\boldsymbol{\nu}$) across individuals.

means <- extract(random, what = "alpha")
means
#> [1]  0.7022074 -0.1530578 -0.1572907  0.6886382  0.5126782 -0.4849197
covariances <- extract(random, what = "tau_sqr")
covariances
#>               [,1]          [,2]          [,3]          [,4]         [,5]
#> [1,]  0.0117386324  0.0084607670 -0.0007749491 -1.110998e-03 -0.004490997
#> [2,]  0.0084607670  0.0147962728 -0.0020873559  2.637241e-04 -0.003466690
#> [3,] -0.0007749491 -0.0020873559  0.0080762011  4.133316e-03 -0.004035007
#> [4,] -0.0011109976  0.0002637241  0.0041333156  9.079855e-03 -0.004483530
#> [5,] -0.0044909967 -0.0034666899 -0.0040350067 -4.483530e-03  0.072407364
#> [6,]  0.0017923246 -0.0018873642 -0.0024451854 -6.762128e-05 -0.045091031
#>               [,6]
#> [1,]  1.792325e-03
#> [2,] -1.887364e-03
#> [3,] -2.445185e-03
#> [4,] -6.762128e-05
#> [5,] -4.509103e-02
#> [6,]  9.072989e-02

Finally, we compare the meta-analytic population estimates to the known generating values.

beta_pop_mean
#> [1]  0.6794612 -0.1445571 -0.1946483  0.6367930
beta_pop_cov
#>              [,1]          [,2]          [,3]         [,4]
#> [1,] 1.668398e-02  0.0099324179  0.0003451996 1.140625e-05
#> [2,] 9.932418e-03  0.0147696609 -0.0006384169 8.493977e-04
#> [3,] 3.451996e-04 -0.0006384169  0.0099154757 5.231290e-03
#> [4,] 1.140625e-05  0.0008493977  0.0052312899 1.323857e-02

nu_mu
#> [1]  0.5 -0.5
nu_sigma
#>       [,1]  [,2]
#> [1,]  0.10 -0.05
#> [2,] -0.05  0.10

Summary

This vignette demonstrates a two-stage hierarchical estimation approach for dynamic systems: 1. individual-level DT-VAR estimation with stabilized measurement error, and
2. population-level meta-analysis of person-specific dynamics and means.

References

Hunter, M. D. (2017). State space modeling in an open source, modular, structural equation modeling environment. Structural Equation Modeling: A Multidisciplinary Journal, 25(2), 307–324. https://doi.org/10.1080/10705511.2017.1369354

Neale, M. C., Hunter, M. D., Pritikin, J. N., Zahery, M., Brick, T. R., Kirkpatrick, R. M., Estabrook, R., Bates, T. C., Maes, H. H., & Boker, S. M. (2015). OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika, 81(2), 535–549. https://doi.org/10.1007/s11336-014-9435-8

R Core Team. (2024). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/