Meta-Regression with Distal Outcome

Dynamics Description

The Stable Persistence with Baseline-Moderated Autoregression process represents a bivariate dynamic system in which two latent psychological constructs (e.g., positive and negative affect) exhibit within-construct persistence over time through autoregressive dynamics. The transition matrix is diagonal, implying that each construct evolves according to its own self-regulatory process and there are no cross-lagged (reciprocal) influences between the constructs in the systematic dynamics.

Between-person heterogeneity in persistence is captured via a time-invariant baseline covariate $x_i \in \left\{ 0, 1 \right\}$ with one value per individual. The individual-specific transition matrix is modeled as $\begin{equation} \mathrm{vec} \left( \boldsymbol{\beta}_i \right) = \mathrm{vec} \left( \boldsymbol{\beta} \left( x_i \right) \right) = \mathrm{vec} \left( \boldsymbol{\beta}_0 \right) + \mathrm{vec} \left( \boldsymbol{\beta}_1 \right) x_i, \end{equation}$ so that individuals with $x_i = 0$ follows $\boldsymbol{\beta}_0$ , whereas individuals with $x_i = 1$ follow $\boldsymbol{\beta}_0 + \boldsymbol{\beta}_1$ . Under the current specification, $\boldsymbol{\beta}_1$ increases the diagonal autoregressive parameters, implying that the $x_i = 1$ group exhibits greater persistence—deviations from an individual’s equilibrium decay more slowly—while remaining dynamically stable.

Between-person heterogeneity in baseline levels is also captured via the same time-invariant covariate $x_i \in \left\{ 0, 1 \right\}$ through the person-specific measurement intercept vector $\begin{equation} \boldsymbol{\nu}_i = \boldsymbol{\nu}\left(x_i\right) = \boldsymbol{\nu}_0 + \boldsymbol{\nu}_1 x_i, \end{equation}$ so that individuals with $x_i = 0$ follow $\boldsymbol{\nu}_0$ , whereas individuals with $x_i = 1$ follow $\boldsymbol{\nu}_0 + \boldsymbol{\nu}_1$ .

In addition to explaining between-person differences in the DT-VAR parameters via the baseline covariate $x_i$ , we also include a distal outcome $z_i$ measured once per individual. Conceptually, $z_i$ can be interpreted as a later outcome (e.g., symptom severity, functioning, or substance use) whose between-person differences are partly explained by (a) each person’s estimated dynamic and mean parameters and (b) $x_i$ .

The process noise covariance allows for small disturbances that may be correlated across constructs, permitting coordinated innovations even though the lagged dynamics are decoupled. Measurement errors are assumed to be minimal and symmetric across indicators.

Model

The measurement model is given by $\begin{equation} \mathbf{y}_{i, t} = \boldsymbol{\nu}_{i} + \boldsymbol{\Lambda} \boldsymbol{\eta}_{i, t} + \boldsymbol{\varepsilon}_{i, t}, \quad \mathrm{with} \quad \boldsymbol{\varepsilon}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \boldsymbol{\Theta} \right) \end{equation}$ where $\mathbf{y}_{i, t}$ , $\boldsymbol{\eta}_{i, t}$ , and $\boldsymbol{\varepsilon}_{i, t}$ are random variables and $\boldsymbol{\nu}_{i}$ , $\boldsymbol{\Lambda}$ , and $\boldsymbol{\Theta}$ are model parameters. $\mathbf{y}_{i, t}$ represents a vector of observed random variables, $\boldsymbol{\eta}_{i, t}$ a vector of latent random variables, and $\boldsymbol{\varepsilon}_{i, t}$ a vector of random measurement errors, at time $t$ and individual $i$ . $\boldsymbol{\nu}_{i}$ denotes a vector of person-specific intercepts while $\boldsymbol{\Lambda}$ denotes a matrix of factor loadings, and $\boldsymbol{\Theta}$ the covariance matrix of $\boldsymbol{\varepsilon}$ that is invariant across individuals. In this model, $\boldsymbol{\Lambda}$ is an identity matrix and $\boldsymbol{\Theta}$ is a symmetric matrix.

The dynamic structure is given by $\begin{equation} \boldsymbol{\eta}_{i, t} = \boldsymbol{\beta}_{i} \boldsymbol{\eta}_{i, t - 1} + \boldsymbol{\zeta}_{i, t}, \quad \mathrm{with} \quad \boldsymbol{\zeta}_{i, t} \sim \mathcal{N} \left( \mathbf{0}, \boldsymbol{\Psi} \right) \end{equation}$ where $\boldsymbol{\eta}_{i, t}$ , $\boldsymbol{\eta}_{i, t - 1}$ , and $\boldsymbol{\zeta}_{i, t}$ are random variables, and $\boldsymbol{\beta}_{i}$ , and $\boldsymbol{\Psi}$ are model parameters. Here, $\boldsymbol{\eta}_{i, t}$ is a vector of latent variables at time $t$ and individual $i$ , $\boldsymbol{\eta}_{i, t - 1}$ represents a vector of latent variables at time $t - 1$ and individual $i$ , and $\boldsymbol{\zeta}_{i, t}$ represents a vector of dynamic noise at time $t$ and individual $i$ . $\boldsymbol{\beta}_{i}$ is a matrix of autoregression and cross regression coefficients for individual $i$ , and $\boldsymbol{\Psi}$ the covariance matrix of $\boldsymbol{\zeta}_{i, t}$ that is invariant across all individuals. In this model, $\boldsymbol{\Psi}$ is a symmetric matrix.

Distal outcome model

Let $z_i$ denote a distal outcome observed once per individual $i$ . We model $z_i$ as a linear function of (a) the person-specific DT-VAR parameters and (b) the baseline covariate $x_i$ :

$\begin{equation} z_i = \kappa + \boldsymbol{\phi}^{\prime} \mathbf{w}_i + \omega x_i + \xi_i, \quad \mathrm{with} \quad \xi_i \sim \mathcal{N}(0, \psi), \end{equation}$

where $\kappa$ is an intercept, $\boldsymbol{\phi}$ is a vector of regression coefficients, $\omega$ is the direct effect of $x_i$ on $z_i$ , and $\psi$ is the residual variance of the distal outcome. The predictor vector $\mathbf{w}_i$ stacks the person-specific DT-VAR coefficients and intercepts used for prediction. In this vignette we use

$\begin{equation} \mathbf{w}_i = \left[ \mathrm{vec}(\boldsymbol{\beta}_i)^{\prime}, \; \boldsymbol{\nu}_i^{\prime} \right]^{\prime}, \end{equation}$

so $\mathbf{w}_i$ has length $p^2 + p$ (here $4 + 2 = 6$ ).

Data Generation

Notation

Let $t = 1000$ be the number of time points and $n = 1000$ be the number of individuals. We simulate a total of time $= 11000$ points per individual, discarding the first $10000$ as burn-in. The analysis uses the final $1000$ measurement occasions.

Let the measurement model intercept vector $\boldsymbol{\nu}$ when $X = 0$ be

$\begin{equation} \left( \begin{array}{c} 0.5 \\ -0.5 \\ \end{array} \right) . \end{equation}$

Let the measurement model intercept vector $\boldsymbol{\nu}$ when $X = 1$ be

$\begin{equation} \left( \begin{array}{c} 0.75 \\ -0.75 \\ \end{array} \right) . \end{equation}$

Let the covariance matrix be

$\begin{equation} \left( \begin{array}{cc} 0.1 & -0.05 \\ -0.05 & 0.1 \\ \end{array} \right) . \end{equation}$

Let the factor loadings matrix $\boldsymbol{\Lambda}$ be given by

$\begin{equation} \boldsymbol{\Lambda} = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right) . \end{equation}$

Let the measurement error covariance matrix $\boldsymbol{\Theta}$ be given by

$\begin{equation} \boldsymbol{\Theta} = \left( \begin{array}{cc} 0.5 & 0 \\ 0 & 0.5 \\ \end{array} \right) . \end{equation}$

Let the initial condition $\boldsymbol{\eta}_{0}$ be given by

$\begin{equation} \boldsymbol{\eta}_{0} \sim \mathcal{N} \left( \boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}, \boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0} \right) . \end{equation}$

$\boldsymbol{\mu}_{\boldsymbol{\eta} \mid 0}$ and $\boldsymbol{\Sigma}_{\boldsymbol{\eta} \mid 0}$ are functions of $\boldsymbol{\alpha}$ and $\boldsymbol{\beta}$ .

Let the transition matrix $\boldsymbol{\beta}$ when $X = 0$ be

$\begin{equation} \left( \begin{array}{cc} 0.5 & 0 \\ 0 & 0.5 \\ \end{array} \right) . \end{equation}$

Let the transition matrix $\boldsymbol{\beta}$ when $X = 1$ be

$\begin{equation} \left( \begin{array}{cc} 0.75 & 0 \\ 0 & 0.75 \\ \end{array} \right) . \end{equation}$

Let the covariance matrix be

$\begin{equation} \left( \begin{array}{cccc} 0.02 & 0.01 & 0 & 0 \\ 0.01 & 0.015 & 0 & 0 \\ 0 & 0 & 0.01 & 0.005 \\ 0 & 0 & 0.005 & 0.015 \\ \end{array} \right) . \end{equation}$

Let the intercept vector $\boldsymbol{\alpha}$ be fixed to a zero vector.

The SimNuN and SimBetaN functions from the simStateSpace package generate random intercept vectors and transition matrices from the multivariate normal distribution. Note that the SimBetaN function generates transition matrices that are weakly stationary with an option to set lower and upper bounds.

Let the dynamic process noise $\boldsymbol{\Psi}$ be given by

$\begin{equation} \boldsymbol{\Psi} = \left( \begin{array}{cc} 0.2 & -0.05 \\ -0.05 & 0.18 \\ \end{array} \right) . \end{equation}$

R Function Arguments

n
#> [1] 1000
time
#> [1] 11000
burnin
#> [1] 10000
# first mu0 in the list of length n
mu0[[1]]
#> [1] 0 0
# first sigma0 in the list of length n
sigma0[[1]]
#>              [,1]         [,2]
#> [1,]  0.262246668 -0.001346401
#> [2,] -0.001346401  0.308495216
# first sigma0_l in the list of length n
sigma0_l[[1]] # sigma0_l <- t(chol(sigma0))
#>              [,1]      [,2]
#> [1,]  0.512100252 0.0000000
#> [2,] -0.002629174 0.5554172
alpha
#> [[1]]
#> [1] 0 0
# first beta in the list of length n
beta[[1]]
#>            [,1]     [,2]
#> [1,] 0.42483430 0.221745
#> [2,] 0.04454242 0.644272
# first psi in the list of length n
psi[[1]]
#>       [,1]  [,2]
#> [1,]  0.20 -0.05
#> [2,] -0.05  0.18
psi_l[[1]] # psi_l <- t(chol(psi))
#>            [,1]      [,2]
#> [1,]  0.4472136 0.0000000
#> [2,] -0.1118034 0.4092676
# first nu in the list of length n
nu[[1]]
#> [1]  0.2385858 -0.4148773
lambda
#> [[1]]
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1
# first theta in the list of length n
theta[[1]]
#>      [,1] [,2]
#> [1,]  0.5  0.0
#> [2,]  0.0  0.5
theta_l[[1]] # theta_l <- t(chol(theta))
#>           [,1]      [,2]
#> [1,] 0.7071068 0.0000000
#> [2,] 0.0000000 0.7071068
# distal outcome parameters
kappa_z
#> [1] 10
phi_z
#>      [,1] [,2] [,3] [,4] [,5] [,6]
#> [1,]    5    5    5    5    5    5
omega_z
#> [1] 0.15
psi_z
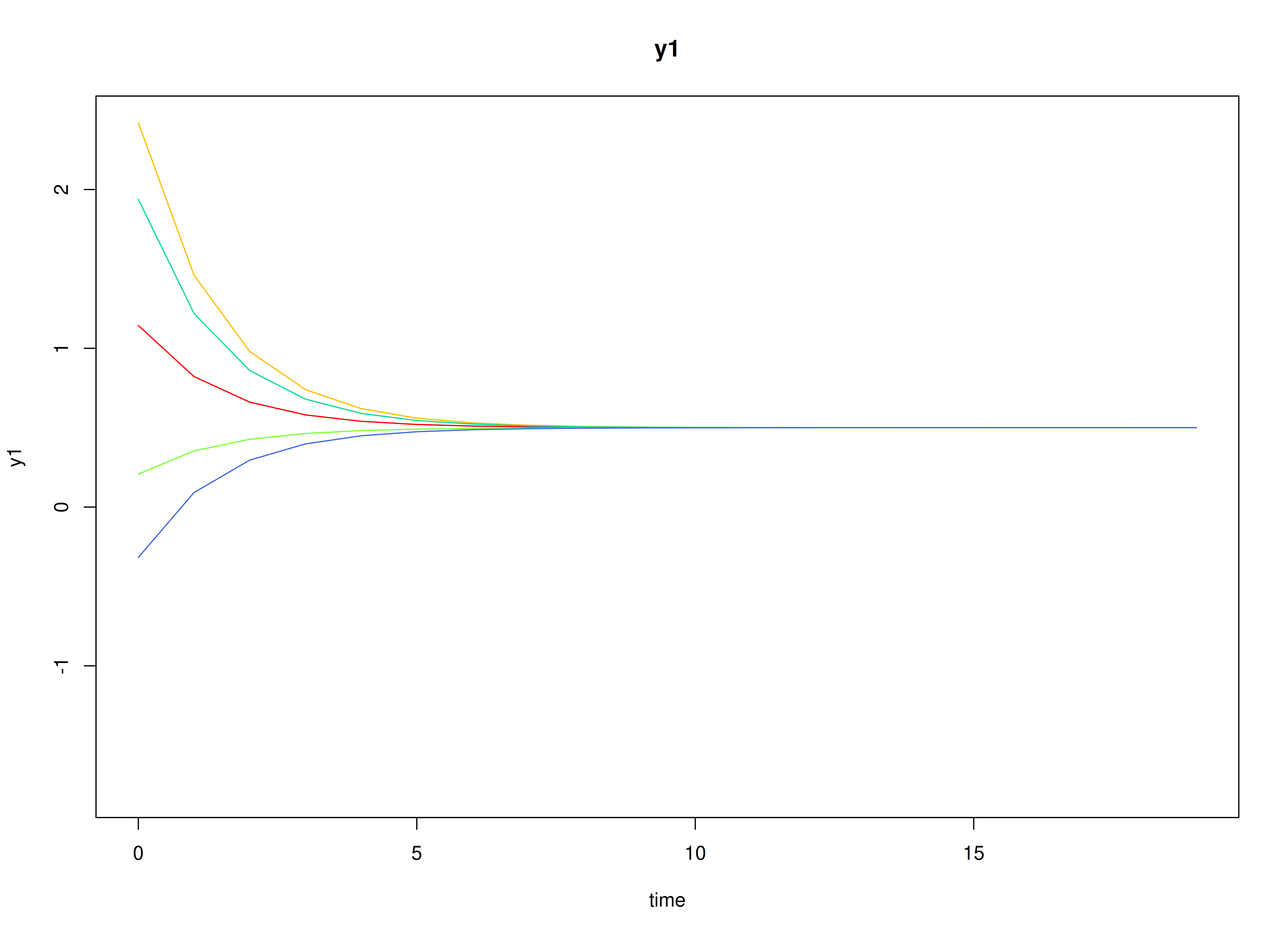
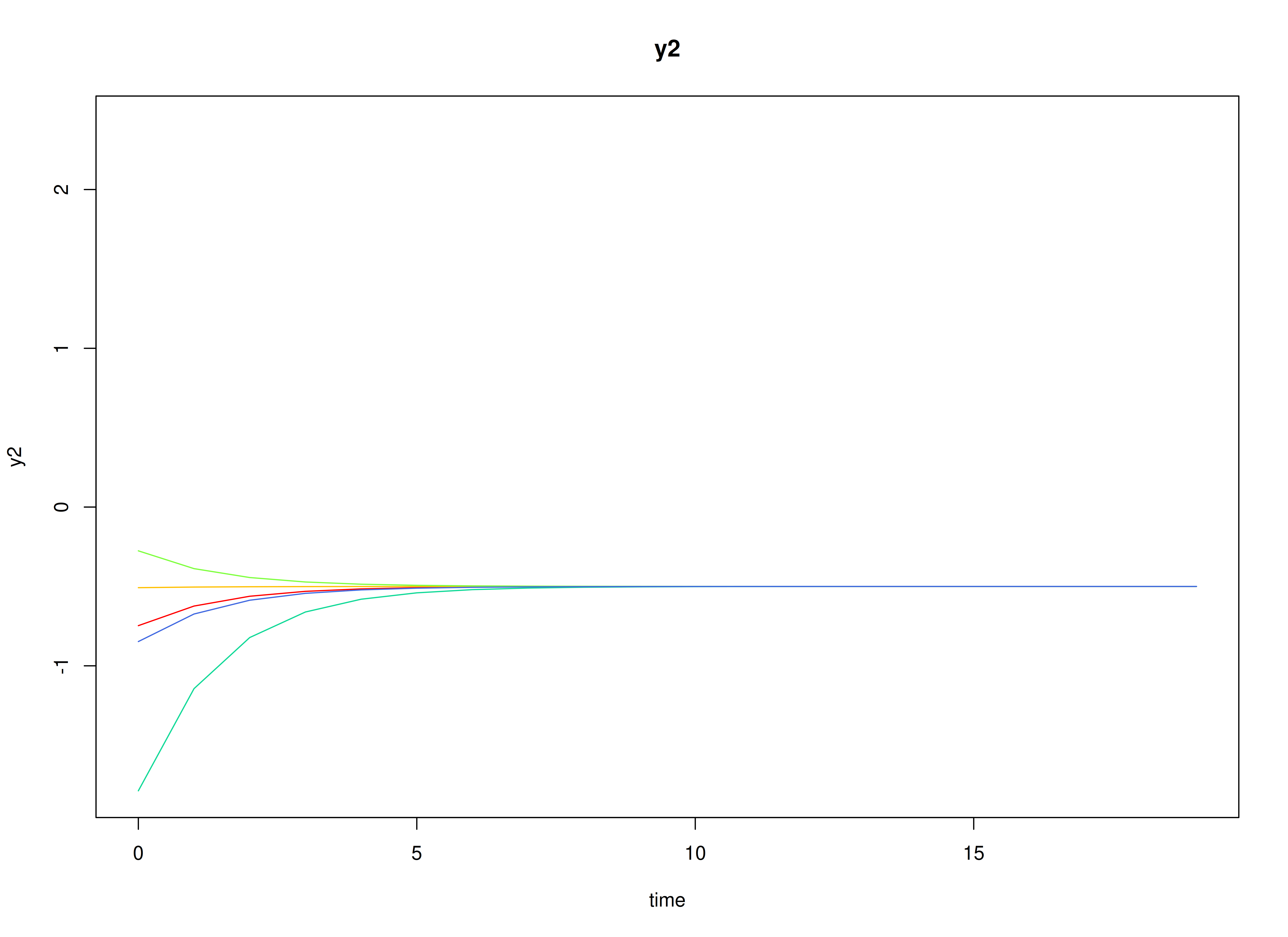
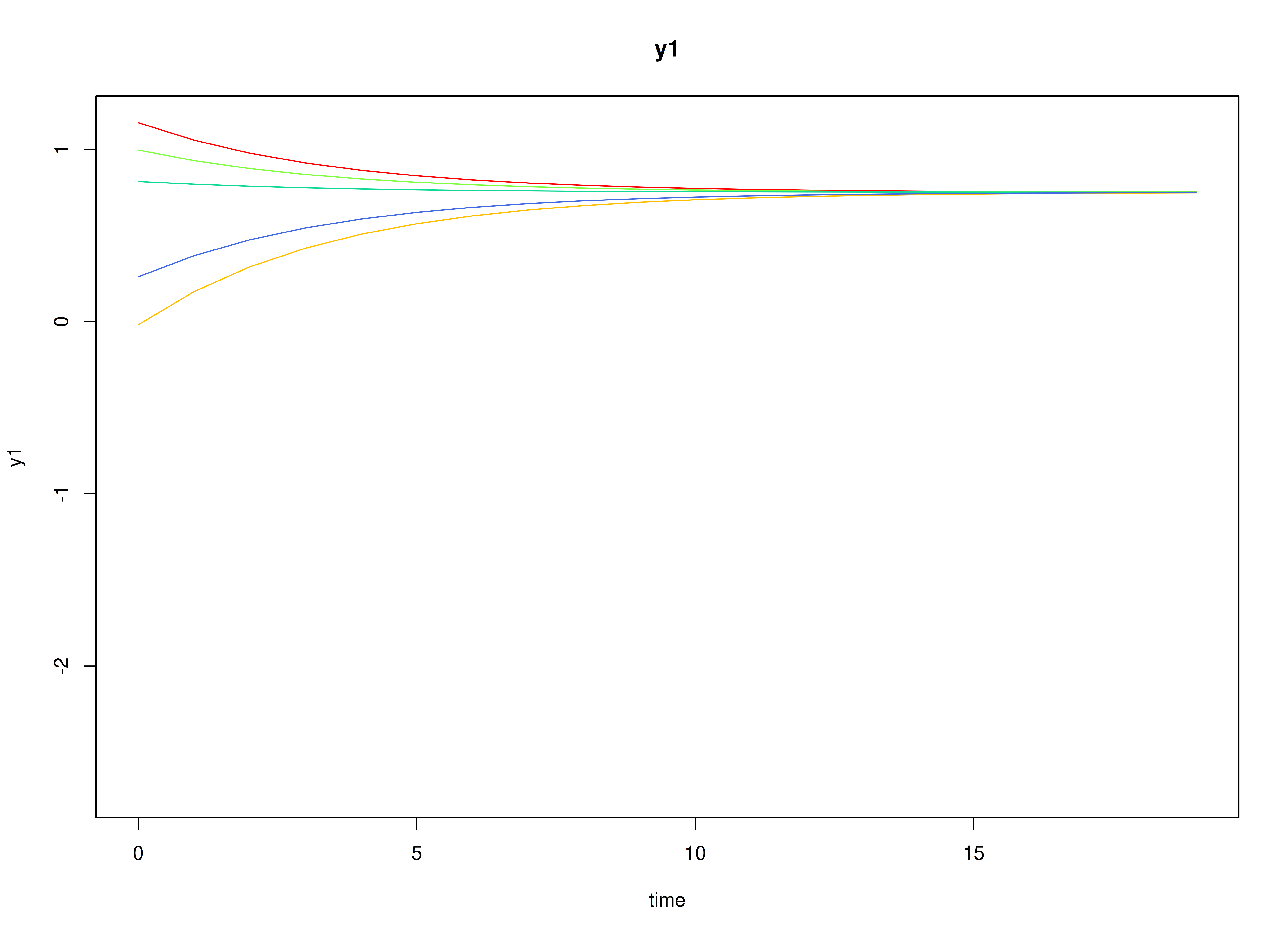
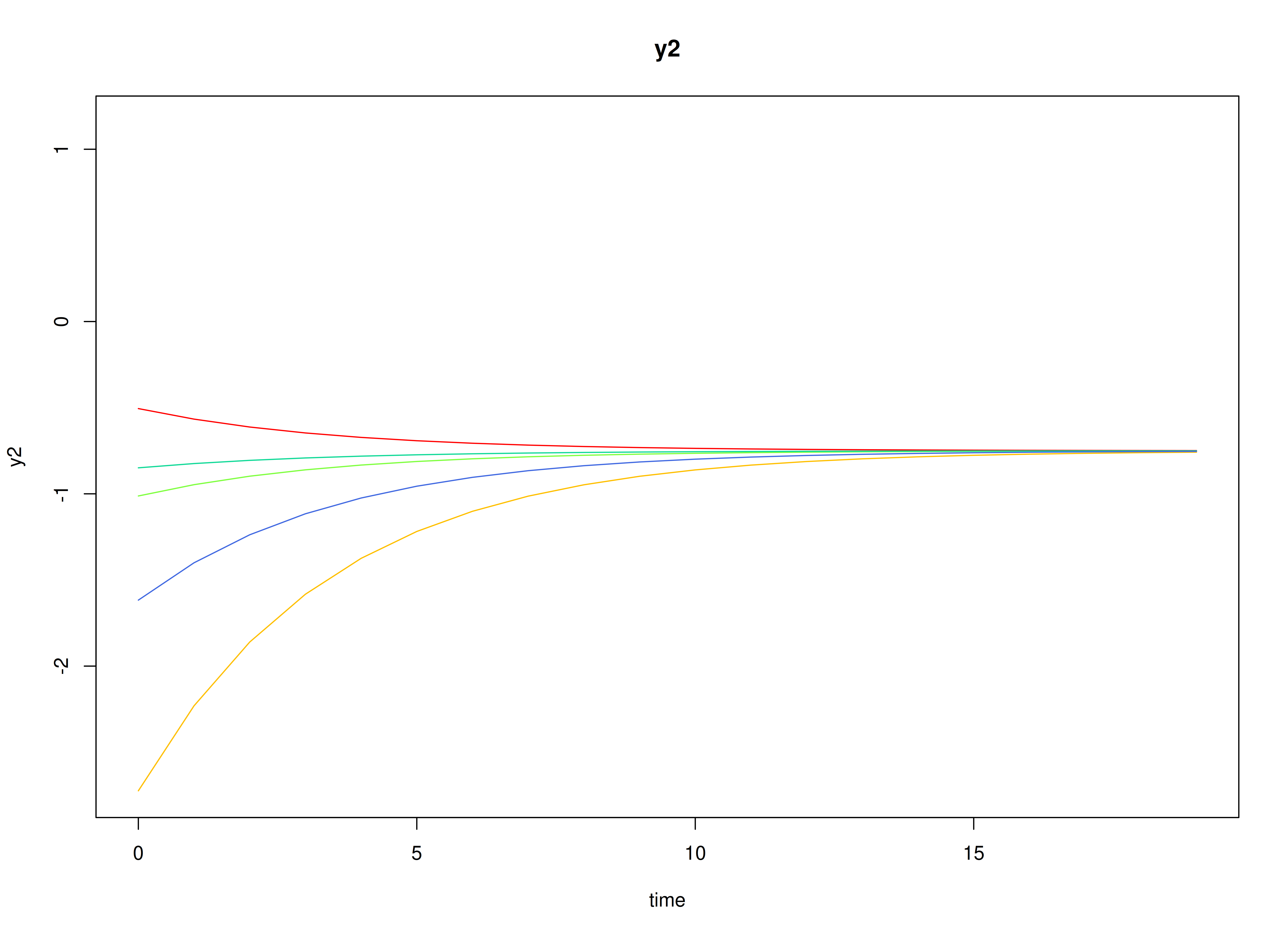
#> [1] 0.45

Visualizing the Dynamics Without Process Noise and Measurement Error (n = 5 with Different Initial Condition)

$X = 0$

$X = 1$

Using the `SimSSMIVary` Function from the `simStateSpace` Package to Simulate Data

library(simStateSpace)
sim <- SimSSMIVary(
  n = n,
  time = time,
  mu0 = mu0,
  sigma0_l = sigma0_l,
  alpha = alpha,
  beta = beta,
  psi_l = psi_l,
  nu = nu,
  lambda = lambda,
  theta_l = theta_l
)
data <- as.data.frame(sim, burnin = burnin)
head(data)
#>   id time         y1         y2
#> 1  1    0  0.2872498 -0.6916122
#> 2  1    1  0.2706470 -1.9931501
#> 3  1    2 -0.3722643 -1.7091924
#> 4  1    3 -0.9400761 -0.6043939
#> 5  1    4  0.1432300 -0.1997853
#> 6  1    5 -0.8617044 -1.4859587
plot(sim, burnin = burnin)

Model Fitting

library(OpenMx)
library(fitDTVARMxID)

The FitDTVARMxID function fits a DT-VAR model on each individual $i$ . To set up the estimation, we first provide starting values for each parameter matrix.

Autoregressive Parameters (`beta`)

We initialize the autoregressive coefficient matrix $\boldsymbol{\beta}$ with the true values used in simulation.

beta_values <- beta

Intercepts (`nu`)

The intercept vector $\boldsymbol{\nu}$ is initialized with starting values.

nu_values <- nu

LDL’-parameterized covariance matrices

Covariances such as psi and theta are estimated using the LDL’ decomposition of a positive definite covariance matrix. The decomposition expresses a covariance matrix $\Sigma$ as

$\begin{equation} \boldsymbol{\Sigma} = \left( \mathbf{L} + \mathbf{I} \right) \mathrm{diag} \left( \mathrm{Softplus} \left( \mathbf{d}_{uc} \right) \right) \left( \mathbf{L} + \mathbf{I} \right)^{\prime}, \end{equation}$

where:

$\mathbf{L}$ is a strictly lower-triangular matrix of free parameters (l_mat_strict),
$\mathbf{I}$ is the identity matrix,
$\mathbf{d}_{uc}$ is an unconstrained vector,
$\mathrm{Softplus} \left(\mathbf{d}_{uc} \right) = \log \left(1 + \exp \left( \mathbf{d}_{uc} \right) \right)$ ensures strictly positive diagonal entries.

The LDL() function extracts this decomposition from a positive definite covariance matrix. It returns:

d_uc: unconstrained diagonal parameters, equal to InvSoftplus(d_vec),
d_vec: diagonal entries, equal to Softplus(d_uc),
l_mat_strict: the strictly lower-triangular factor.

sigma <- matrix(
  data = c(1.0, 0.5, 0.5, 1.0),
  nrow = 2,
  ncol = 2
)

ldl_sigma <- LDL(sigma)
d_uc <- ldl_sigma$d_uc
l_mat_strict <- ldl_sigma$l_mat_strict
I <- diag(2)
sigma_reconstructed <- (l_mat_strict + I) %*% diag(log1p(exp(d_uc)), 2) %*% t(l_mat_strict + I)
sigma_reconstructed
#>      [,1] [,2]
#> [1,]  1.0  0.5
#> [2,]  0.5  1.0

Process Noise Covariance Matrix (`psi`)

Starting values for the process noise covariance matrix $\boldsymbol{\Psi}$ are given below, with corresponding LDL’ parameters.

psi_values <- psi[[1]]
ldl_psi_values <- LDL(psi_values)
psi_d_values <- ldl_psi_values$d_uc
psi_l_values <- ldl_psi_values$l_mat_strict

psi_d_values
#> [1] -1.507772 -1.701853

psi_l_values
#>       [,1] [,2]
#> [1,]  0.00    0
#> [2,] -0.25    0

Measurement Error Covariance Matrix (`theta`)

Starting values for the measurement error covariance matrix $\boldsymbol{\Theta}$ are given below, with corresponding LDL’ parameters.

theta_values <- theta[[1]]
ldl_theta_values <- LDL(theta_values)
theta_d_values <- ldl_theta_values$d_uc
theta_l_values <- ldl_theta_values$l_mat_strict

theta_d_values
#> [1] -0.4327521 -0.4327521

theta_l_values
#>      [,1] [,2]
#> [1,]    0    0
#> [2,]    0    0

Initial mean vector (`mu_0`) and covariance matrix (`sigma_0`)

The initial mean vector $\boldsymbol{\mu_0}$ and covariance matrix $\boldsymbol{\Sigma_0}$ are fixed using mu0 and sigma0.

mu0_values <- mu0

sigma0_values <- lapply(
  X = sigma0,
  FUN = LDL
)
sigma0_d_values <- lapply(
  X = sigma0_values,
  FUN = function(i) {
    i$d_uc
  }
)
sigma0_l_values <- lapply(
  X = sigma0_values,
  FUN = function(i) {
    i$l_mat_strict
  }
)

`FitDTVARMxID`

fit <- FitDTVARMxID(
  data = data,
  observed = c("y1", "y2"),
  id = "id",
  beta_values = beta_values,
  psi_d_values = psi_d_values,
  psi_l_values = psi_l_values,
  nu_values = nu_values,
  theta_d_values = theta_d_values,
  mu0_values = mu0_values,
  sigma0_d_values = sigma0_d_values,
  sigma0_l_values = sigma0_l_values,
  ncores = parallel::detectCores()
)

Parameter estimates

head(summary(fit))
#> Error in `object$coefficients`:
#> ! $ operator is invalid for atomic vectors

Proportion of converged cases

converged(
  fit,
  theta_tol = 0.01,
  prop = TRUE
)
#> Error in `x$output`:
#> ! $ operator is invalid for atomic vectors

Fixed-Effect Meta-Analysis of Measurement Error

When fitting DT-VAR models per person, separating process noise ( $\boldsymbol{\Psi}$ ) from measurement error ( $\boldsymbol{\Theta}$ ) can be unstable for some individuals. To stabilize inference, we first pool the person-level $\boldsymbol{\Theta}_{i}$ estimates from only the converged fits using a fixed-effect meta-analysis. This yields a high-precision estimate of the common measurement-error covariance that we will then hold fixed in a second pass of model fitting.

What the code does: - Selects individuals that converged and whose $\boldsymbol{\Theta}_i$ diagonals exceed a small threshold (theta_tol), filtering out near-zero or ill-conditioned solutions. - Extracts each person’s LDL’ diagonal parameters for $\boldsymbol{\Theta}_i$ and their sampling covariance matrices. - Computes the inverse-variance-weighted pooled estimate (fixed effect), returning it on the same LDL’ parameterization used by FitDTVARMxID().

library(metaVAR)
fixed_theta <- MetaVARMx(
  fit,
  random = FALSE, # TRUE by default
  effects = FALSE, # TRUE by default
  cov_meas = TRUE, # FALSE by default
  theta_tol = 0.01,
  ncores = parallel::detectCores()
)
#> Error in `x$output`:
#> ! $ operator is invalid for atomic vectors

You can read summary(fixed_theta) as providing the pooled (fixed) measurement-error scale that is common across persons. If individual instruments truly share the same reliability structure, fixing $\boldsymbol{\Theta}$ to this pooled value improves stability and often reduces bias in the dynamic parameters.

Note: Fixed-effect pooling assumes a common $\boldsymbol{\Theta}$ across individuals.

coef(fixed_theta)
#> Error:
#> ! object 'fixed_theta' not found
summary(fixed_theta)
#> Error:
#> ! object 'fixed_theta' not found

theta_d_values <- coef(fixed_theta)
#> Error:
#> ! object 'fixed_theta' not found

Refit the model with fixed measurement error covariance matrix

We refit the individual models using the pooled $\boldsymbol{\Theta}$ as a fixed measurement-error covariance matrix.

fit <- FitDTVARMxID(
  data = data,
  observed = c("y1", "y2"),
  id = "id",
  beta_values = beta_values,
  psi_d_values = psi_d_values,
  psi_l_values = psi_l_values,
  nu_values = nu_values,
  theta_fixed = TRUE,
  theta_d_values = theta_d_values,
  mu0_values = mu0_values,
  sigma0_d_values = sigma0_d_values,
  sigma0_l_values = sigma0_l_values,
  ncores = parallel::detectCores()
)

With $\boldsymbol{\Theta}$ fixed, the re-estimation focuses on the dynamic structure ( $\boldsymbol{\beta}$ , $\boldsymbol{\Psi}$ ) and intercepts ( $\boldsymbol{\nu}$ ). In practice, this often increases the proportion of converged fits and yields more stable cross-lag estimates.

Proportion of converged cases

converged(
  fit,
  prop = TRUE
)
#> [1] 1

Mixed-Effects Meta-Analysis of Person-Specific Dynamics and Means

Having stabilized $\boldsymbol{\Theta}$ , we synthesize the person-specific estimates to recover population-level effects, between-person variability, and systematic covariate-related differences. We fit a mixed-effects meta-analytic model in which each individual’s estimate is weighted by its within-person sampling uncertainty, random effects capture residual heterogeneity across individuals, and fixed effects quantify the association between covariate $X$ and the person-specific dynamic parameters.

distal <- MetaVARMx(
  fit,
  x = x,
  z = z,
  effects = TRUE,
  int_meas = TRUE,
  robust_v = FALSE,
  robust = TRUE,
  ncores = parallel::detectCores()
)

summary(distal)
#> [1] 0
#> Call:
#> MetaVARMx(object = fit, x = x, z = z, effects = TRUE, int_meas = TRUE, 
#>     robust_v = FALSE, robust = TRUE, ncores = parallel::detectCores())
#> 
#> CI type = "normal"
#>                  est     se         z      p    2.5%   97.5%
#> alpha[1,1]    0.5063 0.0064   78.6559 0.0000  0.4937  0.5189
#> alpha[2,1]    0.0032 0.0060    0.5334 0.5938 -0.0086  0.0149
#> alpha[3,1]    0.0172 0.0054    3.2169 0.0013  0.0067  0.0277
#> alpha[4,1]    0.5361 0.0058   92.9339 0.0000  0.5248  0.5474
#> alpha[5,1]    0.5149 0.0143   36.0934 0.0000  0.4870  0.5429
#> alpha[6,1]   -0.5073 0.0144  -35.3517 0.0000 -0.5354 -0.4792
#> gamma[1,1]    0.2315 0.0086   26.9642 0.0000  0.2147  0.2484
#> gamma[2,1]   -0.0077 0.0080   -0.9618 0.3362 -0.0233  0.0080
#> gamma[3,1]   -0.0128 0.0069   -1.8496 0.0644 -0.0264  0.0008
#> gamma[4,1]    0.2121 0.0075   28.1216 0.0000  0.1973  0.2268
#> gamma[5,1]    0.2400 0.0204   11.7696 0.0000  0.2001  0.2800
#> gamma[6,1]   -0.2581 0.0205  -12.5909 0.0000 -0.2982 -0.2179
#> kappa[1,1]   10.0685 0.1230   81.8617 0.0000  9.8274 10.3096
#> phi[1,1]      4.8709 0.1506   32.3339 0.0000  4.5756  5.1661
#> phi[1,2]      4.8876 0.1626   30.0532 0.0000  4.5689  5.2064
#> phi[1,3]      5.2444 0.1798   29.1615 0.0000  4.8919  5.5969
#> phi[1,4]      5.0425 0.1625   31.0343 0.0000  4.7240  5.3610
#> phi[1,5]      4.9467 0.0735   67.2725 0.0000  4.8026  5.0908
#> phi[1,6]      4.9818 0.0726   68.6228 0.0000  4.8395  5.1241
#> omega[1,1]    0.1777 0.0696    2.5546 0.0106  0.0414  0.3140
#> psi[1,1]      0.4132 0.0185   22.3612 0.0000  0.3770  0.4494
#> tau_sqr[1,1]  0.0145 0.0008   17.4456 0.0000  0.0128  0.0161
#> tau_sqr[2,1]  0.0063 0.0006   10.9101 0.0000  0.0051  0.0074
#> tau_sqr[3,1] -0.0007 0.0005   -1.5515 0.1208 -0.0016  0.0002
#> tau_sqr[4,1] -0.0006 0.0005   -1.1381 0.2551 -0.0016  0.0004
#> tau_sqr[5,1] -0.0009 0.0014   -0.6798 0.4966 -0.0037  0.0018
#> tau_sqr[6,1] -0.0007 0.0014   -0.4882 0.6254 -0.0034  0.0020
#> tau_sqr[2,2]  0.0122 0.0007   17.2863 0.0000  0.0108  0.0136
#> tau_sqr[3,2] -0.0015 0.0004   -3.5763 0.0003 -0.0023 -0.0007
#> tau_sqr[4,2] -0.0020 0.0005   -4.4177 0.0000 -0.0029 -0.0011
#> tau_sqr[5,2] -0.0005 0.0013   -0.4200 0.6745 -0.0030  0.0020
#> tau_sqr[6,2]  0.0013 0.0013    0.9729 0.3306 -0.0013  0.0038
#> tau_sqr[3,3]  0.0081 0.0005   15.5427 0.0000  0.0071  0.0091
#> tau_sqr[4,3]  0.0032 0.0004    7.7866 0.0000  0.0024  0.0041
#> tau_sqr[5,3] -0.0019 0.0011   -1.7091 0.0874 -0.0040  0.0003
#> tau_sqr[6,3]  0.0009 0.0011    0.8007 0.4233 -0.0013  0.0030
#> tau_sqr[4,4]  0.0103 0.0006   16.4191 0.0000  0.0091  0.0116
#> tau_sqr[5,4] -0.0008 0.0012   -0.6424 0.5206 -0.0031  0.0016
#> tau_sqr[6,4] -0.0004 0.0012   -0.3501 0.7262 -0.0028  0.0019
#> tau_sqr[5,5]  0.1003 0.0046   21.6342 0.0000  0.0912  0.1093
#> tau_sqr[6,5] -0.0540 0.0037  -14.4871 0.0000 -0.0613 -0.0467
#> tau_sqr[6,6]  0.1014 0.0047   21.5508 0.0000  0.0922  0.1107
#> i_sqr[1,1]    0.9171 0.0044  210.5337 0.0000  0.9086  0.9257
#> i_sqr[2,1]    0.9252 0.0039  238.5004 0.0000  0.9176  0.9328
#> i_sqr[3,1]    0.8586 0.0076  112.3987 0.0000  0.8436  0.8736
#> i_sqr[4,1]    0.9011 0.0053  170.4208 0.0000  0.8907  0.9114
#> i_sqr[5,1]    0.9839 0.0007 1341.5918 0.0000  0.9824  0.9853
#> i_sqr[6,1]    0.9819 0.0008 1182.1651 0.0000  0.9802  0.9835

Normal Theory Confidence Intervals

confint(distal, level = 0.95, lb = FALSE)
#>                     2.5 %        97.5 %
#> alpha[1,1]    0.493652888  0.5188834876
#> alpha[2,1]   -0.008550077  0.0149440240
#> alpha[3,1]    0.006730426  0.0277203078
#> alpha[4,1]    0.524790400  0.5474028167
#> alpha[5,1]    0.486980032  0.5429054302
#> alpha[6,1]   -0.535438931 -0.4791862951
#> gamma[1,1]    0.214713458  0.2483742581
#> gamma[2,1]   -0.023275782  0.0079519084
#> gamma[3,1]   -0.026406411  0.0007648680
#> gamma[4,1]    0.197276119  0.2268350359
#> gamma[5,1]    0.200065523  0.2800114878
#> gamma[6,1]   -0.298241177 -0.2178964766
#> kappa[1,1]    9.827430883 10.3095585435
#> phi[1,1]      4.575604328  5.1661117575
#> phi[1,2]      4.568875459  5.2063833962
#> phi[1,3]      4.891945001  5.5969077479
#> phi[1,4]      4.724047794  5.3609642215
#> phi[1,5]      4.802594257  5.0908362957
#> phi[1,6]      4.839505319  5.1240793866
#> omega[1,1]    0.041358823  0.3140216798
#> psi[1,1]      0.376985908  0.4494204630
#> tau_sqr[1,1]  0.012833628  0.0160822524
#> tau_sqr[2,1]  0.005129043  0.0073754426
#> tau_sqr[3,1] -0.001618641  0.0001882717
#> tau_sqr[4,1] -0.001554772  0.0004124352
#> tau_sqr[5,1] -0.003668881  0.0017792270
#> tau_sqr[6,1] -0.003391027  0.0020386089
#> tau_sqr[2,2]  0.010814035  0.0135798831
#> tau_sqr[3,2] -0.002252142 -0.0006575118
#> tau_sqr[4,2] -0.002932415 -0.0011300465
#> tau_sqr[5,2] -0.003038169  0.0019658482
#> tau_sqr[6,2] -0.001270119  0.0037741291
#> tau_sqr[3,3]  0.007073791  0.0091152560
#> tau_sqr[4,3]  0.002429951  0.0040647273
#> tau_sqr[5,3] -0.004045741  0.0002766297
#> tau_sqr[6,3] -0.001277733  0.0030428442
#> tau_sqr[4,4]  0.009106618  0.0115754576
#> tau_sqr[5,4] -0.003125286  0.0015823354
#> tau_sqr[6,4] -0.002795820  0.0019482999
#> tau_sqr[5,5]  0.091178132  0.1093446142
#> tau_sqr[6,5] -0.061255568 -0.0466561896
#> tau_sqr[6,6]  0.092221353  0.1106738694
#> i_sqr[1,1]    0.908587865  0.9256638321
#> i_sqr[2,1]    0.917600741  0.9328071444
#> i_sqr[3,1]    0.843624915  0.8735686609
#> i_sqr[4,1]    0.890710435  0.9114364422
#> i_sqr[5,1]    0.982435747  0.9853104751
#> i_sqr[6,1]    0.980225466  0.9834811824

confint(distal, level = 0.99, lb = FALSE)
#>                     0.5 %        99.5 %
#> alpha[1,1]    0.489688873  0.5228475022
#> alpha[2,1]   -0.012241268  0.0186352148
#> alpha[3,1]    0.003432677  0.0310180572
#> alpha[4,1]    0.521237732  0.5509554849
#> alpha[5,1]    0.478193515  0.5516919471
#> alpha[6,1]   -0.544276860 -0.4703483655
#> gamma[1,1]    0.209424963  0.2536627531
#> gamma[2,1]   -0.028182008  0.0128581341
#> gamma[3,1]   -0.030675328  0.0050337853
#> gamma[4,1]    0.192632076  0.2314790783
#> gamma[5,1]    0.187505101  0.2925719093
#> gamma[6,1]   -0.310864244 -0.2052734094
#> kappa[1,1]    9.751683138 10.3853062888
#> phi[1,1]      4.482828887  5.2588871986
#> phi[1,2]      4.468715702  5.3065431524
#> phi[1,3]      4.781187326  5.7076654226
#> phi[1,4]      4.623980971  5.4610310447
#> phi[1,5]      4.757308151  5.1361224020
#> phi[1,6]      4.794795493  5.1687892130
#> omega[1,1]   -0.001479617  0.3568601194
#> psi[1,1]      0.365605615  0.4608007563
#> tau_sqr[1,1]  0.012323232  0.0165926483
#> tau_sqr[2,1]  0.004776108  0.0077283776
#> tau_sqr[3,1] -0.001902528  0.0004721583
#> tau_sqr[4,1] -0.001863843  0.0007215058
#> tau_sqr[5,1] -0.004524841  0.0026351868
#> tau_sqr[6,1] -0.004244084  0.0028916664
#> tau_sqr[2,2]  0.010379489  0.0140144294
#> tau_sqr[3,2] -0.002502677 -0.0004069771
#> tau_sqr[4,2] -0.003215587 -0.0008468739
#> tau_sqr[5,2] -0.003824357  0.0027520363
#> tau_sqr[6,2] -0.002062628  0.0045666380
#> tau_sqr[3,3]  0.006753054  0.0094359933
#> tau_sqr[4,3]  0.002173109  0.0043215693
#> tau_sqr[5,3] -0.004724835  0.0009557234
#> tau_sqr[6,3] -0.001956545  0.0037216561
#> tau_sqr[4,4]  0.008718735  0.0119633405
#> tau_sqr[5,4] -0.003864907  0.0023219562
#> tau_sqr[6,4] -0.003541175  0.0026936551
#> tau_sqr[5,5]  0.088323970  0.1121987755
#> tau_sqr[6,5] -0.063549297 -0.0443624609
#> tau_sqr[6,6]  0.089322252  0.1135729699
#> i_sqr[1,1]    0.905905036  0.9283466610
#> i_sqr[2,1]    0.915211641  0.9351962436
#> i_sqr[3,1]    0.838920411  0.8782731644
#> i_sqr[4,1]    0.887454144  0.9146927339
#> i_sqr[5,1]    0.981984094  0.9857621276
#> i_sqr[6,1]    0.979713956  0.9839926925

Robust Confidence Intervals

confint(distal, level = 0.95, lb = FALSE, robust = TRUE)
#>                     2.5 %        97.5 %
#> alpha[1,1]    0.492944595  0.5195917805
#> alpha[2,1]   -0.008494761  0.0148887080
#> alpha[3,1]    0.006700797  0.0277499373
#> alpha[4,1]    0.524023881  0.5481693354
#> alpha[5,1]    0.486915003  0.5429704588
#> alpha[6,1]   -0.534437865 -0.4801873611
#> gamma[1,1]    0.214578423  0.2485092930
#> gamma[2,1]   -0.023244588  0.0079207151
#> gamma[3,1]   -0.026375126  0.0007335834
#> gamma[4,1]    0.197098131  0.2270130237
#> gamma[5,1]    0.200045188  0.2800318224
#> gamma[6,1]   -0.298322174 -0.2178154790
#> kappa[1,1]    9.824584684 10.3124047426
#> phi[1,1]      4.562818624  5.1788974615
#> phi[1,2]      4.564542836  5.2107160185
#> phi[1,3]      4.882014085  5.6068386634
#> phi[1,4]      4.724835565  5.3601764501
#> phi[1,5]      4.807932498  5.0854980556
#> phi[1,6]      4.845673021  5.1179116844
#> omega[1,1]    0.038822014  0.3165584885
#> psi[1,1]      0.376919687  0.4494866846
#> tau_sqr[1,1]  0.012883399  0.0160324817
#> tau_sqr[2,1]  0.005148381  0.0073561045
#> tau_sqr[3,1] -0.001616444  0.0001860743
#> tau_sqr[4,1] -0.001602037  0.0004597007
#> tau_sqr[5,1] -0.003571122  0.0016814678
#> tau_sqr[6,1] -0.003360174  0.0020077563
#> tau_sqr[2,2]  0.010777277  0.0136166413
#> tau_sqr[3,2] -0.002243788 -0.0006658662
#> tau_sqr[4,2] -0.002888545 -0.0011739160
#> tau_sqr[5,2] -0.002986262  0.0019139407
#> tau_sqr[6,2] -0.001159516  0.0036635260
#> tau_sqr[3,3]  0.007091238  0.0090978092
#> tau_sqr[4,3]  0.002450824  0.0040438542
#> tau_sqr[5,3] -0.004017274  0.0002481625
#> tau_sqr[6,3] -0.001204225  0.0029693362
#> tau_sqr[4,4]  0.009148899  0.0115331766
#> tau_sqr[5,4] -0.003274891  0.0017319410
#> tau_sqr[6,4] -0.002841785  0.0019942648
#> tau_sqr[5,5]  0.090626296  0.1098964496
#> tau_sqr[6,5] -0.061530330 -0.0463814275
#> tau_sqr[6,6]  0.091411423  0.1114837986
#> i_sqr[1,1]    0.908849478  0.9254022189
#> i_sqr[2,1]    0.917521700  0.9328861851
#> i_sqr[3,1]    0.843852495  0.8733410807
#> i_sqr[4,1]    0.891139045  0.9110078320
#> i_sqr[5,1]    0.982348406  0.9853978155
#> i_sqr[6,1]    0.980083323  0.9836233250

confint(distal, level = 0.99, lb = FALSE, robust = TRUE)
#>                     0.5 %        99.5 %
#> alpha[1,1]    0.488758019  0.5237783568
#> alpha[2,1]   -0.012168570  0.0185625173
#> alpha[3,1]    0.003393737  0.0310569970
#> alpha[4,1]    0.520230355  0.5519628613
#> alpha[5,1]    0.478108053  0.5517774092
#> alpha[6,1]   -0.542961236 -0.4716639892
#> gamma[1,1]    0.209247497  0.2538402190
#> gamma[2,1]   -0.028141013  0.0128171391
#> gamma[3,1]   -0.030634213  0.0049926704
#> gamma[4,1]    0.192398161  0.2317129940
#> gamma[5,1]    0.187478377  0.2925986335
#> gamma[6,1]   -0.310970693 -0.2051669605
#> kappa[1,1]    9.747942598 10.3890468285
#> phi[1,1]      4.466025624  5.2756904620
#> phi[1,2]      4.463021672  5.3122371833
#> phi[1,3]      4.768135891  5.7207168580
#> phi[1,4]      4.625016278  5.4599957375
#> phi[1,5]      4.764323788  5.1291067653
#> phi[1,6]      4.802901227  5.1606834783
#> omega[1,1]   -0.004813548  0.3601940511
#> psi[1,1]      0.365518585  0.4608877862
#> tau_sqr[1,1]  0.012388642  0.0165272385
#> tau_sqr[2,1]  0.004801523  0.0077029630
#> tau_sqr[3,1] -0.001899640  0.0004692704
#> tau_sqr[4,1] -0.001925960  0.0007836233
#> tau_sqr[5,1] -0.004396363  0.0025067094
#> tau_sqr[6,1] -0.004203537  0.0028511193
#> tau_sqr[2,2]  0.010331180  0.0140627378
#> tau_sqr[3,2] -0.002491698 -0.0004179567
#> tau_sqr[4,2] -0.003157933 -0.0009045282
#> tau_sqr[5,2] -0.003756139  0.0026838182
#> tau_sqr[6,2] -0.001917271  0.0044212809
#> tau_sqr[3,3]  0.006775983  0.0094130643
#> tau_sqr[4,3]  0.002200541  0.0042941374
#> tau_sqr[5,3] -0.004687423  0.0009183111
#> tau_sqr[6,3] -0.001859939  0.0036250502
#> tau_sqr[4,4]  0.008774301  0.0119077739
#> tau_sqr[5,4] -0.004061522  0.0025185713
#> tau_sqr[6,4] -0.003601583  0.0027540633
#> tau_sqr[5,5]  0.087598736  0.1129240101
#> tau_sqr[6,5] -0.063910396 -0.0440013623
#> tau_sqr[6,6]  0.088257825  0.1146373973
#> i_sqr[1,1]    0.906248854  0.9280028429
#> i_sqr[2,1]    0.915107764  0.9353001206
#> i_sqr[3,1]    0.839219502  0.8779740733
#> i_sqr[4,1]    0.888017433  0.9141294447
#> i_sqr[5,1]    0.981869310  0.9858769123
#> i_sqr[6,1]    0.979527149  0.9841794996

Profile-Likelihood Confidence Intervals

confint(distal, level = 0.95, lb = TRUE)
#>                     2.5 %        97.5 %
#> alpha[1,1]    0.493533789  0.5188411733
#> alpha[2,1]   -0.008599334  0.0149220664
#> alpha[3,1]    0.006655337  0.0277238659
#> alpha[4,1]    0.524714125  0.5473868726
#> alpha[5,1]    0.486817767  0.5430889902
#> alpha[6,1]   -0.535637437 -0.4790035352
#> gamma[1,1]    0.214707255  0.2484173874
#> gamma[2,1]   -0.023370016  0.0079789122
#> gamma[3,1]   -0.026479184  0.0007970891
#> gamma[4,1]    0.197224711  0.2268923419
#> gamma[5,1]    0.199774678  0.2802789494
#> gamma[6,1]   -0.298502376 -0.2176391819
#> kappa[1,1]    9.826019226 10.3109723758
#> phi[1,1]      4.574258680  5.1674463046
#> phi[1,2]      4.566738501  5.2085187661
#> phi[1,3]      4.890385376  5.5984658094
#> phi[1,4]      4.721956787  5.3630567983
#> phi[1,5]      4.802360647  5.0910700071
#> phi[1,6]      4.839266962  5.1243174203
#> omega[1,1]    0.040580326  0.3148002690
#> psi[1,1]      0.378855379  0.4516598471
#> tau_sqr[1,1]  0.012921787  0.0161877626
#> tau_sqr[2,1]  0.005170312  0.0074265960
#> tau_sqr[3,1] -0.001621520  0.0001949178
#> tau_sqr[4,1] -0.001564935  0.0004152058
#> tau_sqr[5,1] -0.003689808  0.0017885326
#> tau_sqr[6,1] -0.003411928  0.0020413544
#> tau_sqr[2,2]  0.010892028  0.0136714864
#> tau_sqr[3,2] -0.002265775 -0.0006602480
#> tau_sqr[4,2] -0.002947700 -0.0011342047
#> tau_sqr[5,2] -0.003051409  0.0019680077
#> tau_sqr[6,2] -0.001268596  0.0037953541
#> tau_sqr[3,3]  0.007134435  0.0091829417
#> tau_sqr[4,3]  0.002453741  0.0040962373
#> tau_sqr[5,3] -0.004070906  0.0002741161
#> tau_sqr[6,3] -0.001280377  0.0030588884
#> tau_sqr[4,4]  0.009175339  0.0116569864
#> tau_sqr[5,4] -0.003136675  0.0015866769
#> tau_sqr[6,4] -0.002812631  0.0019539765
#> tau_sqr[5,5]  0.091645453  0.1099028340
#> tau_sqr[6,5] -0.061641032 -0.0469854953
#> tau_sqr[6,6]  0.092707607  0.1112520902
#> i_sqr[1,1]    0.908202306  0.9253127172
#> i_sqr[2,1]    0.917229963  0.9325033765
#> i_sqr[3,1]    0.842962794  0.8729383601
#> i_sqr[4,1]    0.890228890  0.9110095531
#> i_sqr[5,1]    0.982392042  0.9852649339
#> i_sqr[6,1]    0.980176005  0.9834300087

confint(distal, level = 0.99, lb = TRUE)
#>                     0.5 %        99.5 %
#> alpha[1,1]    0.489508639  0.5227641694
#> alpha[2,1]   -0.012324858  0.0186401998
#> alpha[3,1]    0.003352273  0.0309834409
#> alpha[4,1]    0.521087395  0.5509039215
#> alpha[5,1]    0.478018776  0.5518856307
#> alpha[6,1]   -0.544449482 -0.4701743294
#> gamma[1,1]    0.209417059  0.2537358171
#> gamma[2,1]   -0.028198917  0.0129628107
#> gamma[3,1]   -0.030676539  0.0050926566
#> gamma[4,1]    0.192648524  0.2316062165
#> gamma[5,1]    0.187272288  0.2927961933
#> gamma[6,1]   -0.311125109 -0.2050118950
#> kappa[1,1]    9.750367074 10.3866227072
#> phi[1,1]      4.482176477  5.2595393029
#> phi[1,2]      4.467885947  5.3073731429
#> phi[1,3]      4.779248147  5.7096018038
#> phi[1,4]      4.621970444  5.4618058374
#> phi[1,5]      4.756986633  5.1364437660
#> phi[1,6]      4.794476079  5.1691083264
#> omega[1,1]   -0.002370062  0.3577511258
#> psi[1,1]      0.368981118  0.4648311827
#> tau_sqr[1,1]  0.012480465  0.0167746370
#> tau_sqr[2,1]  0.004845003  0.0078158235
#> tau_sqr[3,1] -0.001907930  0.0004891502
#> tau_sqr[4,1] -0.001881710  0.0007279096
#> tau_sqr[5,1] -0.004558330  0.0026440265
#> tau_sqr[6,1] -0.004279001  0.0029059033
#> tau_sqr[2,2]  0.010514956  0.0141723518
#> tau_sqr[3,2] -0.002523258 -0.0004108417
#> tau_sqr[4,2] -0.003244250 -0.0008530942
#> tau_sqr[5,2] -0.003853019  0.0027677010
#> tau_sqr[6,2] -0.002065900  0.0046029010
#> tau_sqr[3,3]  0.006857113  0.0095562983
#> tau_sqr[4,3]  0.002210483  0.0043743648
#> tau_sqr[5,3] -0.004772630  0.0009491212
#> tau_sqr[6,3] -0.001955367  0.0037578889
#> tau_sqr[4,4]  0.008840703  0.0121067340
#> tau_sqr[5,4] -0.003895420  0.0023351822
#> tau_sqr[6,4] -0.003572978  0.0027031929
#> tau_sqr[5,5]  0.089188638  0.1131804346
#> tau_sqr[6,5] -0.064214275 -0.0449270228
#> tau_sqr[6,6]  0.090201930  0.1145905899
#> i_sqr[1,1]    0.905259355  0.9277448625
#> i_sqr[2,1]    0.914646696  0.9347008329
#> i_sqr[3,1]    0.837763815  0.8772286330
#> i_sqr[4,1]    0.886624948  0.9139752093
#> i_sqr[5,1]    0.981908600  0.9856874805
#> i_sqr[6,1]    0.979627812  0.9839041567

The fixed part of the random-effects model gives pooled means for the person-specific parameters (e.g., $\mathbb{E}[\mathrm{vec}(\boldsymbol{\beta}_i)]$ and $\mathbb{E}[\boldsymbol{\nu}_i]$ ) and fixed effects for how $X$ shifts these parameters.
The random part yields between-person covariances ( $\boldsymbol{\tau}^2$ ) quantifying residual heterogeneity in dynamics and intercepts beyond what is explained by $X$ .
The distal-outcome sub-model yields regression effects linking the distal outcome $z_i$ to the estimated person-specific parameters (via $\boldsymbol{\phi}$ ), a direct effect of $X$ on $z_i$ (via $\omega$ ), and the residual variance $\psi$ .

means <- extract(distal, what = "alpha")
means
#> [1]  0.506268188  0.003196974  0.017225367  0.536096608  0.514942731
#> [6] -0.507312613
covariances <- extract(distal, what = "tau_sqr")
covariances
#>               [,1]          [,2]          [,3]          [,4]          [,5]
#> [1,]  0.0144579404  0.0062522428 -0.0007151847 -0.0005711684 -0.0009448270
#> [2,]  0.0062522428  0.0121969590 -0.0014548271 -0.0020312306 -0.0005361605
#> [3,] -0.0007151847 -0.0014548271  0.0080945236  0.0032473390 -0.0018845558
#> [4,] -0.0005711684 -0.0020312306  0.0032473390  0.0103410376 -0.0007714752
#> [5,] -0.0009448270 -0.0005361605 -0.0018845558 -0.0007714752  0.1002613729
#> [6,] -0.0006762089  0.0012520048  0.0008825555 -0.0004237600 -0.0539558789
#>               [,6]
#> [1,] -0.0006762089
#> [2,]  0.0012520048
#> [3,]  0.0008825555
#> [4,] -0.0004237600
#> [5,] -0.0539558789
#> [6,]  0.1014476111

Finally, we compare the meta-analytic population estimates to the known generating values.

beta_pop_mean
#> [1]  0.608857758 -0.007162951 -0.003195778  0.618151352
beta_pop_cov
#>              [,1]          [,2]         [,3]          [,4]
#> [1,]  0.031250377  0.0084594085 -0.001357726  0.0126662858
#> [2,]  0.008459408  0.0139070808 -0.001129366 -0.0006591882
#> [3,] -0.001357726 -0.0011293659  0.010097588  0.0047962721
#> [4,]  0.012666286 -0.0006591882  0.004796272  0.0281857098

nu_mu
#> [1]  0.625 -0.625
nu_sigma
#>       [,1]  [,2]
#> [1,]  0.10 -0.05
#> [2,] -0.05  0.10

Summary

This vignette demonstrates a two-stage hierarchical estimation approach for dynamic systems: 1. Individual-level DT-VAR estimation with stabilized measurement error. 2. Population-level meta-analysis of person-specific dynamics and means. 3. Estimation and interpretation of covariate effects, where $X$ predicts systematic between-person differences in dynamics and baseline levels. 4. A distal outcome model linking $z_i$ to person-specific dynamic/mean features and to $X$ .

References

Hunter, M. D. (2017). State space modeling in an open source, modular, structural equation modeling environment. Structural Equation Modeling: A Multidisciplinary Journal, 25(2), 307–324. https://doi.org/10.1080/10705511.2017.1369354

Neale, M. C., Hunter, M. D., Pritikin, J. N., Zahery, M., Brick, T. R., Kirkpatrick, R. M., Estabrook, R., Bates, T. C., Maes, H. H., & Boker, S. M. (2015). OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika, 81(2), 535–549. https://doi.org/10.1007/s11336-014-9435-8

R Core Team. (2024). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

Ivan Jacob Agaloos Pesigan

2026-01-07

Dynamics Description

Model

Distal outcome model

Data Generation

Notation

R Function Arguments

Visualizing the Dynamics Without Process Noise and Measurement Error (n = 5 with Different Initial Condition)

$X = 0$

$X = 1$

Using the `SimSSMIVary` Function from the `simStateSpace` Package to Simulate Data

Model Fitting

Autoregressive Parameters (`beta`)

Intercepts (`nu`)

LDL’-parameterized covariance matrices

Process Noise Covariance Matrix (`psi`)

Measurement Error Covariance Matrix (`theta`)

Initial mean vector (`mu_0`) and covariance matrix (`sigma_0`)

`FitDTVARMxID`

Parameter estimates

Proportion of converged cases

Fixed-Effect Meta-Analysis of Measurement Error

Refit the model with fixed measurement error covariance matrix

Proportion of converged cases

Mixed-Effects Meta-Analysis of Person-Specific Dynamics and Means

Normal Theory Confidence Intervals

Robust Confidence Intervals

Profile-Likelihood Confidence Intervals

Summary

References

Meta-Regression with Distal Outcome

Ivan Jacob Agaloos Pesigan

2026-01-07

Dynamics Description

Model

Distal outcome model

Data Generation

Notation

R Function Arguments

Visualizing the Dynamics Without Process Noise and Measurement Error (n = 5 with Different Initial Condition)

X=0X = 0

X=1X = 1

Using the SimSSMIVary Function from the simStateSpace Package to Simulate Data

Model Fitting

Autoregressive Parameters (beta)

Intercepts (nu)

LDL’-parameterized covariance matrices

Process Noise Covariance Matrix (psi)

Measurement Error Covariance Matrix (theta)

Initial mean vector (mu_0) and covariance matrix (sigma_0)

FitDTVARMxID

Parameter estimates

Proportion of converged cases

Fixed-Effect Meta-Analysis of Measurement Error

Refit the model with fixed measurement error covariance matrix

Proportion of converged cases

Mixed-Effects Meta-Analysis of Person-Specific Dynamics and Means

Normal Theory Confidence Intervals

Robust Confidence Intervals

Profile-Likelihood Confidence Intervals

Summary

References

$X = 0$

$X = 1$

Using the `SimSSMIVary` Function from the `simStateSpace` Package to Simulate Data

Autoregressive Parameters (`beta`)

Intercepts (`nu`)

Process Noise Covariance Matrix (`psi`)

Measurement Error Covariance Matrix (`theta`)

Initial mean vector (`mu_0`) and covariance matrix (`sigma_0`)

`FitDTVARMxID`