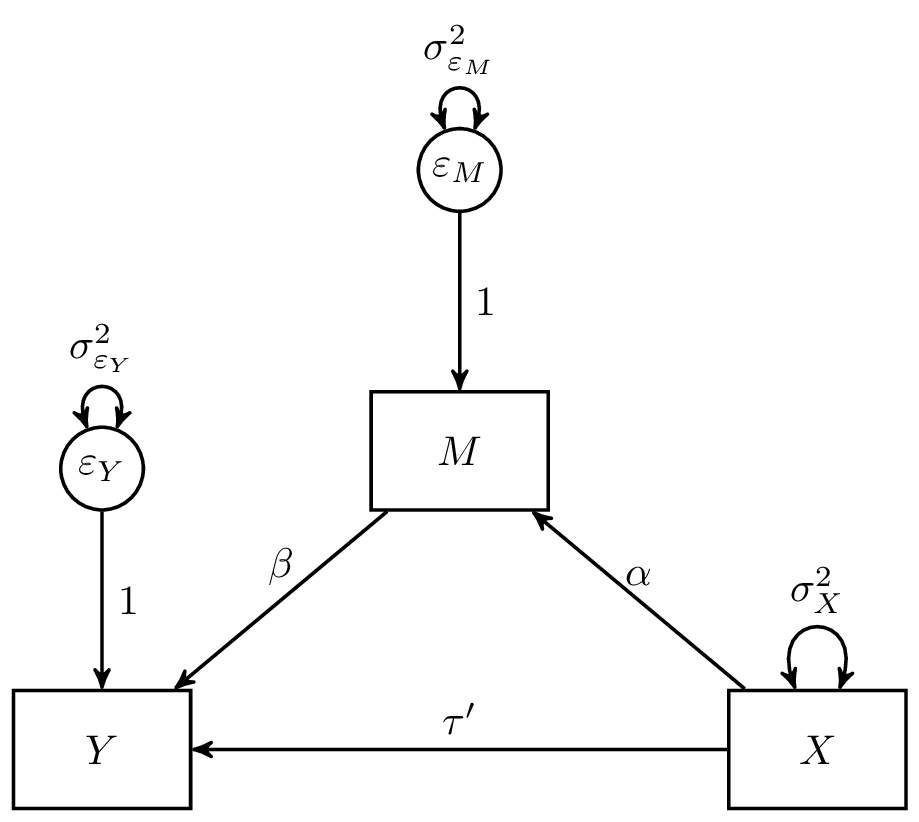
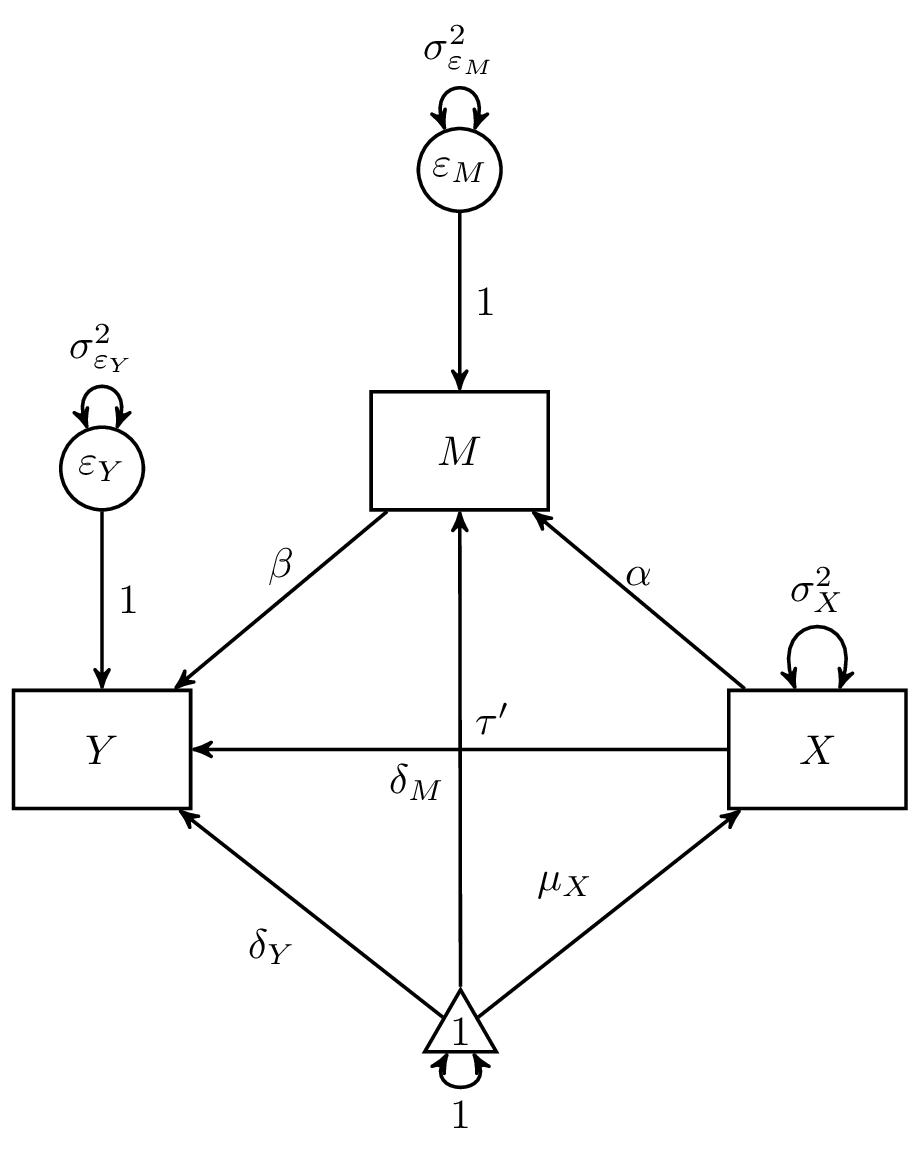
The most basic mediation model involves three variables, \(X\), \(M\), and \(Y\) whose associations are expressed in the following equations
\[\begin{equation} Y = \delta_{Y} + \tau^{\prime}{X} + \beta{M} + \varepsilon_{Y}, \end{equation}\]
\[\begin{equation} M = \delta_{M} + \alpha X + \varepsilon_{M}, \end{equation}\]
where \(\alpha\) represents the effect of the independent variable \(X\) on the mediator variable \(M\); \(\beta\) represents the effect of the mediator variable \(M\) on the dependent variable \(Y\); \(\tau^{\prime}\) represents the effect of the independent variable \(X\) on the dependent variable \(Y\), adjusting for the mediator variable \(M\); \(\delta_{M}\) and \(\delta_{Y}\) are intercepts; and \(\varepsilon_{M}\) and \(\varepsilon_{Y}\) are stochastic error terms. The direct effect, \(\tau^{\prime}\), which is the change in the dependent variable corresponding to one unit change in the independent variable, while the mediator variable is held constant, can be contrasted with the indirect effect (the product of \(\alpha\) and \(\beta\) or \(\alpha \beta\)), which represents the change in the dependent variable via the mediator if the independent variable increases by one unit. See MacKinnon (2008) for more information on the simple mediation model.
Expected Values
\[\begin{equation} \label{eq:expected} \mathbb{E} \left[ \begin{array}{c} {X} \\ {M} \\ {Y} \end{array} \right] = \left[ \begin{array}{c} {\mu}_{X} \\ {\mu}_{M} \\ {\mu}_{Y} \end{array} \right] = \left[ \begin{array}{c} {\mu}_{X} \\ {\delta}_{M} + {\alpha}{\mu}_{X} \\ {\delta}_{Y} + {\tau}^{\prime}{\mu}_{X} + {\beta}{\mu}_{M} \end{array} \right] \end{equation}\]
Model-Implied Variance-Covariance Matrix
\[\begin{equation} \label{eq:Sigma} \boldsymbol{\Sigma} = \left[ \begin{array}{ccc} \sigma_{X}^{2} & & \\ \alpha \sigma_{X}^{2} & \sigma_{M}^{2} = \alpha^2 \sigma_{X}^{2} + \sigma_{\varepsilon_{M}}^{2} & \\ \beta \alpha \sigma_{X}^{2} + \tau^{\prime} \sigma_{X}^{2} & \beta \alpha^{2} \sigma_{X}^{2} + \tau^{\prime} \alpha \sigma_{X}^{2} + \beta \sigma_{\varepsilon_{M}}^{2} & \sigma_{Y}^{2} = \tau^{\prime 2} \sigma_{X}^{2} + \alpha^2 \beta^2 \sigma_{X}^{2} + \beta^2 \sigma_{\varepsilon_{M}}^{2} + 2 \tau^{\prime} \beta \alpha \sigma_{X}^{2} + \sigma_{\varepsilon_{Y}}^{2} \\ \end{array} \right] \end{equation}\]
Error Variances
\[\begin{equation} \label{eq:sigma2eY} \sigma_{\varepsilon_{Y}}^{2} = \sigma_{Y}^{2} - \tau^{\prime 2} \sigma_{X}^{2} - \alpha^2 \beta^2 \sigma_{X}^{2} - \beta^2 \sigma_{\varepsilon_{M}}^{2} - 2 \tau^{\prime} \beta \alpha \sigma_{X}^{2} \end{equation}\]
\[\begin{equation} \label{eq:sigma2eM} \sigma_{\varepsilon_{M}}^{2} = \sigma_{M}^{2} - \alpha^2 \sigma_{X}^{2} \end{equation}\]